Last week we played Doubles Memory to help with the recognition of the doubles. Did you enjoy this game? Do you see the kids increasing in their knowledge and comfort with the doubles? Well, we’re going to build on those skills with this week’s game.
Double the Product Memory game is from RightStart™ Mathematics Level D Second Edition and is similar to last week’s game. This game is a traditional memory game where the players have face down cards, try to find two specific cards, then capture the paired cards. The interesting twist is the definition of pairs. The pairs consist of a number and the double of that number. An example of pairs are 4 and 8, 10 and 20, 27 and 54, 24 and 48, and 45 and 90.
If you have the Multiplication Cards, you’re ready to play. If you don’t have this card deck, you can make the cards using index cards. Use two sets of multiples – one set will be a double of the other. Possible sets are 2s and 4s, 3s and 6s, 4s and 8s, and 5s and 10s. Of course, we could use 1s and 2s, but that’s pretty basic. For today’s game, let’s use the 4s and 8s.
Place the 4s multiples face down in random order in two rows of five. Nearby, do the same with the ten 8s multiples.
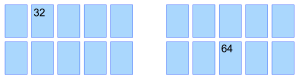
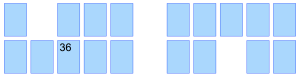
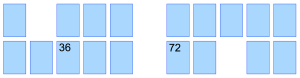
The first player turns over a 4s card, doubles it, and states the doubled amount. Since our first player turned over the 32-card shown below, she says “32 doubled is 64.” She then picks a card that might be the one she’s searching for, the 64-card.
If she finds that card, she takes both cards and gets another turn. If she doesn’t find the double, she turns over both cards in their original place and the second player takes his turn.
The winner is the player with the most cards after all the pairs are found. We recommend playing this game at least twice per set. This allows the child to formulate their strategies and make the connections between the two sets.
So what is this game really about? Most people know the multiples of 1s, 2s, 3s, 5s, and 10s pretty quickly. But if you know the 2s, you can double and find the 4s. And when you know the 4s, you can double and get the 8s. If you know the 3s, the 6s are right there. The only multiples not being reviewed in this game are the 7s and 9s.
A lot of time, children (and many adults) think of multiplication as just facts that have to be memorized. This game provides another method to figure out a fact that may be just out of reach. It gives a child another method to approach their math facts. Don’t know what 8 × 6 is? You know that 4 × 6 = 24 and 24 × 2 = 48. Now 8 × 6 is known!
One final thought: Remember that games don’t need to be played on a table. Kids love to play games on the floor. Or outside on the patio. Or on a blanket on the lawn or beach. Be creative and have fun! Keep in touch, leave us a comment below, and let us know how the games go…..
