There’s a lot of things I love about teaching RightStart Math to my children, but one of the top reasons is this: all the new concepts that I get to learn alongside them. From fractals to check numbers to the mathematics of music to unique patterns in the multiples, we explore a lot of concepts that are new to me. Although I had a perfectly functional elementary mathematics education, I don’t remember it being fun, or innovative, or playful. We marched through our textbooks from point A to point Z without taking time for the scenic route.
Well, it’s summer and we’re going to take time for the scenic route today. Let’s detour to one of those mathematical concepts that maybe aren’t necessary, but that are fun to play with. Ready? I present to you: the fraction series.
Do you know what a fraction series is? I sure didn’t. And you could certainly live the rest of your life without ever needing to know this – but then you would be missing out on something pretty neat.
So here it is: A fraction series is a list of fractions with consecutive numerators and the same denominator. Make sense? No? Another way to describe it is skip counting by fractions. Think about skip counting by thirds: 1/3, 2/3, 3/3.
That was easy, wasn’t it? Let’s try it with something else. How about skip counting by eighths? Off we go: 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, 8/8.
Easy enough. But you might have noticed that not all the fractions in that eighths series were simplified. Think about it. What would happen if you were to simplify all the fractions you could in that list?
Here’s what you would get: 1/8, 1/4, 3/8, 1/2, 5/8, 3/4, 7/8, 1.
And that is the simplified eighths series. Isn’t that neat?!?
Some series, like the fifths and the sevenths, don’t have any simplified fractions except for the final number – 1. But some series are more interesting and require a little more thinking. Simplifying on the fly comes more intuitively to some people than to others. If you’re teaching this concept to your child, and she needs a little more practice visualizing how the simplified series work, you could have her build the different fraction series using fraction chart pieces.
Here’s what the eighths series looks like with the fraction chart pieces – we call this the “fraction stairs of eighths”:

Once your child (and you!) have a basic understanding of skip counting by simplified fractions, you’re ready for the game of Series Solitaire, game F16 in the Math Card Games book! Your goal is to build five fraction series: the 1/4 series, the 1/5 series, the 1/6 series, the 1/8 series, and the 1/10 series.
Before you begin, you’ll need to take a few minutes to set up, because this game requires thirty-three specific cards from the fraction deck. These are the cards you’ll need:
- 1 each of 1/3, 2/3, 1/6, 5/6, 1/8, 3/8, 5/8, 7/8, 1/10, 3/10, 7/10, and 9/10
- 2 each of 1/4, 3/4, 1/5, 2/5, 3/5, 4/5
- 4 each of 1/2
- and 5 1s.
Here’s a visual to help you:

Once you’ve got the cards, shuffle them and deal them in fans of three. If you’d like, you can write the starting fractions on little pieces of paper, so that your player knows where she has to begin.

Now we’re ready to play!
As I mentioned, the goal is to build the series of 1/4, 1/5, 1/6, 1/8, and 1/10. Only the top card of each fan is available for play.
It sounds simple, but this game is a little more challenging than most of our other solitaire games. It’s harder to win, because there are a lot of one-and-only cards – cards that you only have one of, and that can’t be played if they are stuck behind other cards you can’t use yet. So this game has a few special rules that our other solitaire games don’t have.
We’re going to need those rules right off the bat, because my beginning layout is a spectacularly bad one. There’s not a single card I can play. I need a 1/4, 1/5, 1/6, 1/8 or 1/10 to get started, and none of them are available!
So it’s lucky for me that in this game, you can actually move cards around within the fans. Here are the two ways you can do that:
- Any available 1 can be placed onto another available 1 in a fan.
- Any available card in a fan may be placed on another card in a fan, if it immediately precedes it in one of the series. For example, 4/5 is preceded by 3/5. If both of those cards were available, but you couldn’t actually play them yet, because 2/5 is still stuck somewhere else – you could still move the 3/5 onto the 4/5 within the fans. Another example: 1 is preceded by 3/4, 4/5, 5/6, 7/8, and 9/10 – so you could place any of those cards on a 1.
That second rule is a little complicated, but if you’re not getting it, no worries – just watch how it plays out as I go through this game.
For my first move, I’m going to move one 1 onto another 1. There are two 1s available and I could move either one of them onto the other. See them?

I decide to move the 1 in the third row onto the 1 in the upper row.

Immediately that frees up the 1/5 and the 1/6, so I can start two series now:

And now I’ve got lots of options for what to play next. Do you see all the possibilities?
I decide to wrap up the 1/5 series right away:

And for a while, game play is pretty easy. I keep building my series and playing merrily along, until this point:

Uh-oh! Do you see the problem? The game is nearly over, but I’m stuck. I’ve completed the 1/4, 1/5, and 1/6 series. I need either a 3/4 for my eighths series, or a 1/2 for my tenths series. But both of those cards are trapped behind other cards.
I can’t put a 1 on another 1 in a fan, because I don’t have two available 1s. So now the second rule is going to come in handy. I can move any free card onto another free card if the first card precedes the second in a series. Do you see where that’s possible in the layout above?
I can see four possibilities:
- 9/10 precedes 1 in the tenths series
- 4/5 precedes 1 in the fifths series
- 7/8 precedes 1 in the eighths series
- 4/5 precedes the 9/10 in the tenths series
All of those moves are allowable. After thinking it over, I decide that the first move is the most useful, and move the 9/10 over the 1. Then I move the 4/5 on the 9/10 as well. Now the cards look like this:
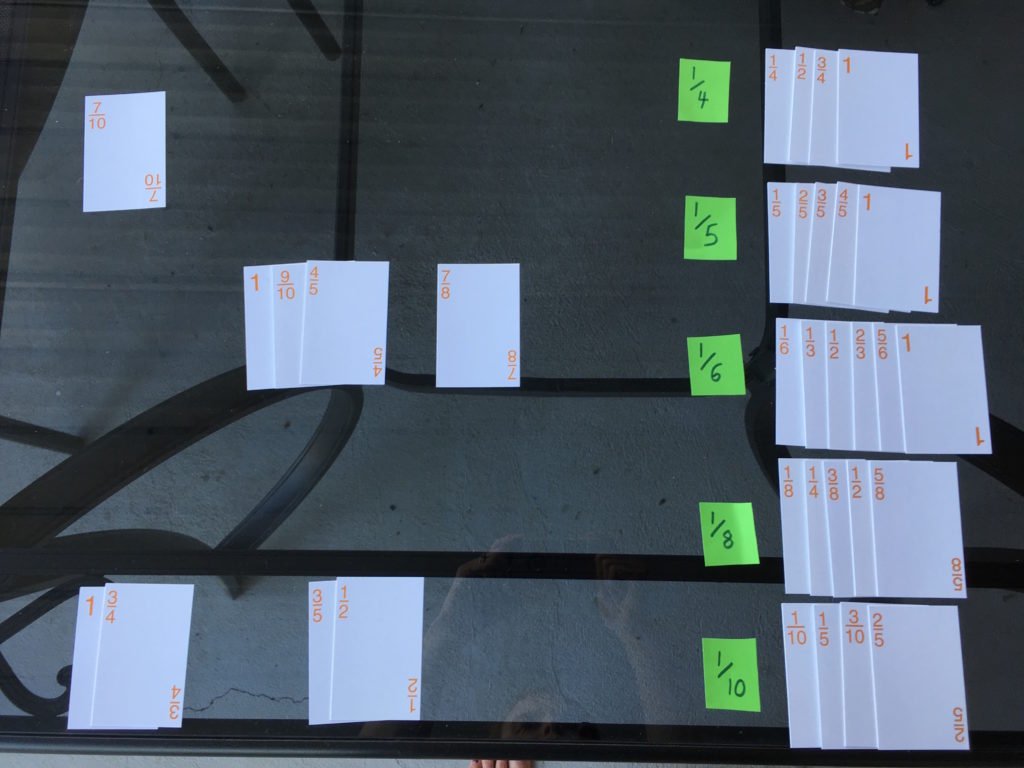
That’s all I need to free up both the 1/2 and the 3/4 cards; and from there it’s an easy coast to the finish line. Here’s my completed game…aren’t those series beautiful?!

And that’s a beauty you never would have seen if you’d stuck to the beaten path. Here’s to taking the scenic route this summer!
