Susan wrote us: “Hello, my son and I are struggling with Lesson 154, with problems 9 & 10. Can we please have an explanation? Love your materials! Thank you.”
Well, Susan, this took me a while to come up with a good clear explanation! Here’s my process of thinking through the problems, including all my errors. I did need to start at the beginning because jumping into your question needed groundwork laid first.
First, I read Lesson 154, Rotating Symmetry in Polyhedra, in RightStart Mathematics: A Hands-On Geometric Approach. The goals of the lesson are to learn about the axes of symmetry, to find the axes of symmetry of the Platonic solids, and to discover some dual relationships. By the way, remember to always look at the lesson’s goals because this helps you know where you’re going for the day.
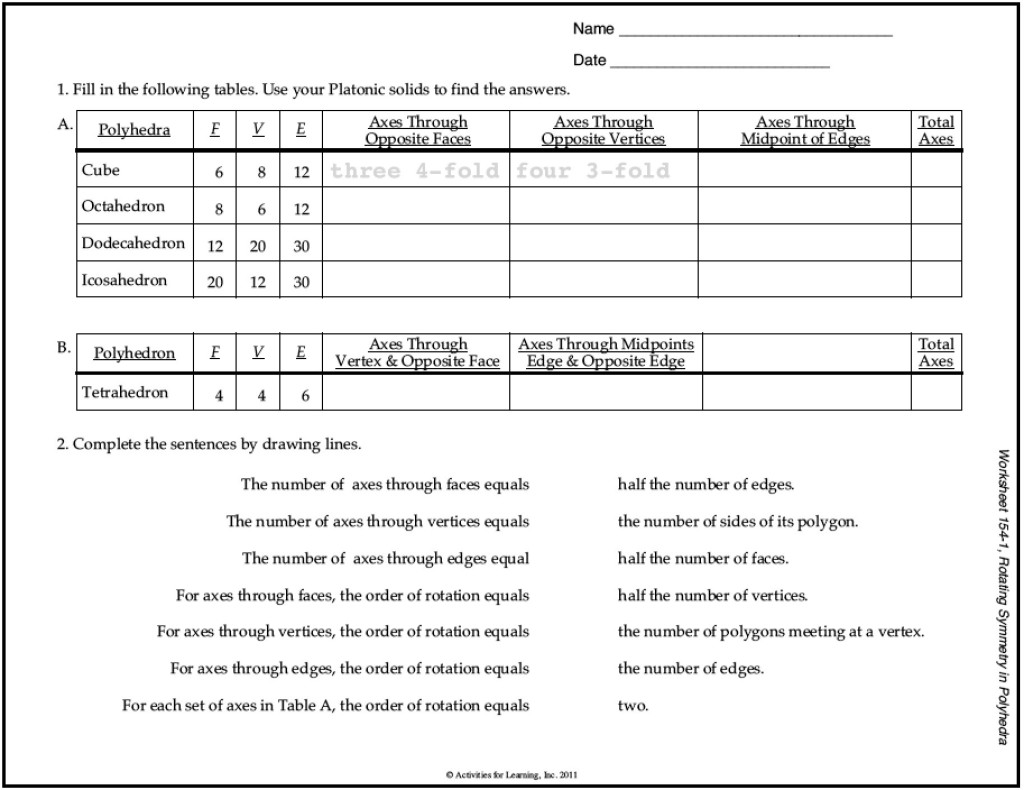
So, that lesson was interesting, but the excitement started when I got to the worksheets. Click on the image to get a better copy of the worksheet.
Problem 1 and 2. Got these without too much struggle. Here’s the first chart filled in.
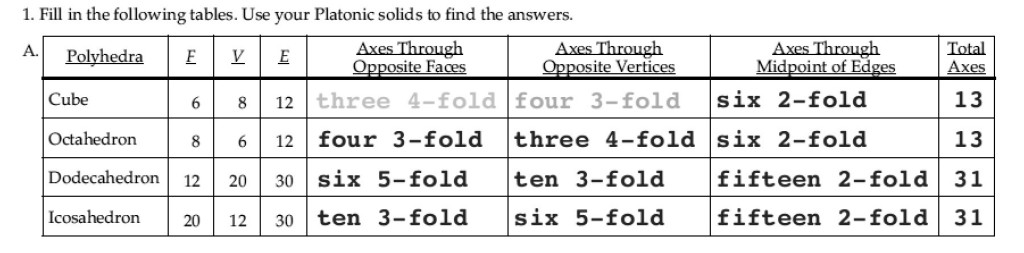
And, yes, I know that if you don’t have the lesson book and aren’t in Level G, this chart’s information doesn’t make a lot of sense. But there are some good ideas in thought processing here…..
Problem 3. If no faces are regular, how many different ways will the package fit into the box? I just mentally played with the image on the worksheet – the package can be rotated around four times. Because it doesn’t have regular (the same) faces, then we can’t flip it upside down and rotate again. That leaves us with four rotations. See the image of the package and the box on the worksheet?
Problem 4. If two sides are square, how many different ways will the package fit into the box? Again, I just mentally played around with it. I did struggle for a minute with the image. Think long package with square ends. Now the package could be put in “feet” first and rotated four times around or it could go in “head” first and rotated another four times. Answer is 4 × 2, which is 8 possible ways to fit the package in the box.
Problem 5. If all the faces are square, how many different ways will the package fit into the box? Following Problem 3 and 4, there are six sides, or faces, that can be each rotated four times: 6 × 4 = 24. Got it.
Problem 6. How many different ways can you can put the octahedron into the box? Here I had to go build myself octahedron out of the geometry panels to play with.

I came up with 3 axes (because I could stand it on three different vertices) × 2 (for top and bottom) × 4 rotations around: 3 × 2 × 4 = 24.
Problem 7 and 8. Easy. 10 sides (as seen the image provided on the worksheet) is a decagon.
Problem 9. How many different ways could you put the dodecahedron into the decagonal prism? Using my previous methods with the cube and octahedron, I have 10 axis (from the chart under Axes Through Opposite Vertices) × 2 (for top and bottom) × 10 rotations…. Wait. This isn’t going to work. The correct answer is 120 and I’m coming up with 200. Something’s wrong.
I went back to the cube and octahedron and looked to see if I could approach this another way.
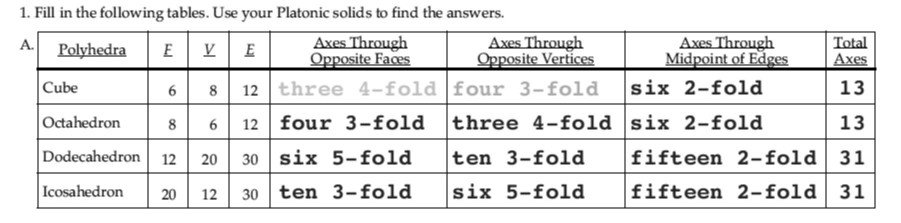
Problem 5, Round 2. Using the table (and my cube in hand), I know that a cube has 6 faces. I know that I need to rotate it four times. Where do I see “four” on in the “cube” row in the chart? Look at Axes through Opposite Vertices: 4. Will that work? 6 faces × 4 axes (through opposite vertices) = 24.
Ok. Now let’s see if that works for the octahedron….
Problem 6, Round 2. I know from playing with the octahedron that there are three axes (and I used that information in Round 1). The chart says there are 3 axes through opposite vertices. Like the cube, I’m going to multiply the axes by the number of faces. Chart says there are 8 faces. And, of course, I can see that in my geometry panel octahedron. 8 faces × 3 axes = 24.
It does work! Let’s try this new approach on the dodecahedron!
Problem 9, Round 2. A dodecahedron has 12 faces. I know this because I know what a dodecahedron is and, well, it’s in the chart! Axes through opposite vertices? 10. The chart says so and I figured this out during my first go-around with this problem. 12 faces x 10 axes = 120!!
I think we’ve got this. Let’s see if we can knock out the last question.
Problem 10. How many different ways could you put the icosahedron into the decagonal prism? Icosahedron has 20 faces (says the chart) and 6 axes through opposite vertices (says the chart). This means we can put into a decagonal prism 20 × 6 times, 120! Wahoo!! Correct answer!!
One final word to the teachers of this lesson: This dialog here is my process. It’s my thinking it through. I share all my errors and starts and stops because I want you to see the process, logic (or lack of logic), and thinking. Read this through, understand it yourself, then guide your student to the correct conclusion.
Might you find another way? Perhaps! Go for it. We’d love to hear all about it!