We just had a student email us with questions about RS2 Level G, Lesson 119. Well, actually, it was Worksheet 119-2, problem 4.
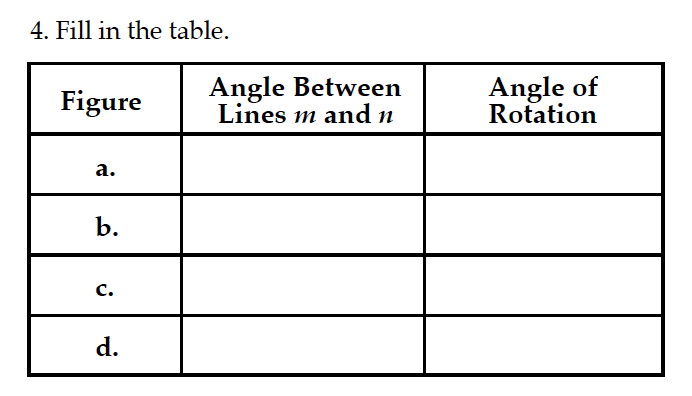
Obviously, we need to see what the problems looks like.
Here is the first problem. We are given an object and are to reflect it about a line, then reflect the new image and find the center of rotation. The original object is at the top of the page in black. The reflections are drawn in blue and the center of rotation is identified.
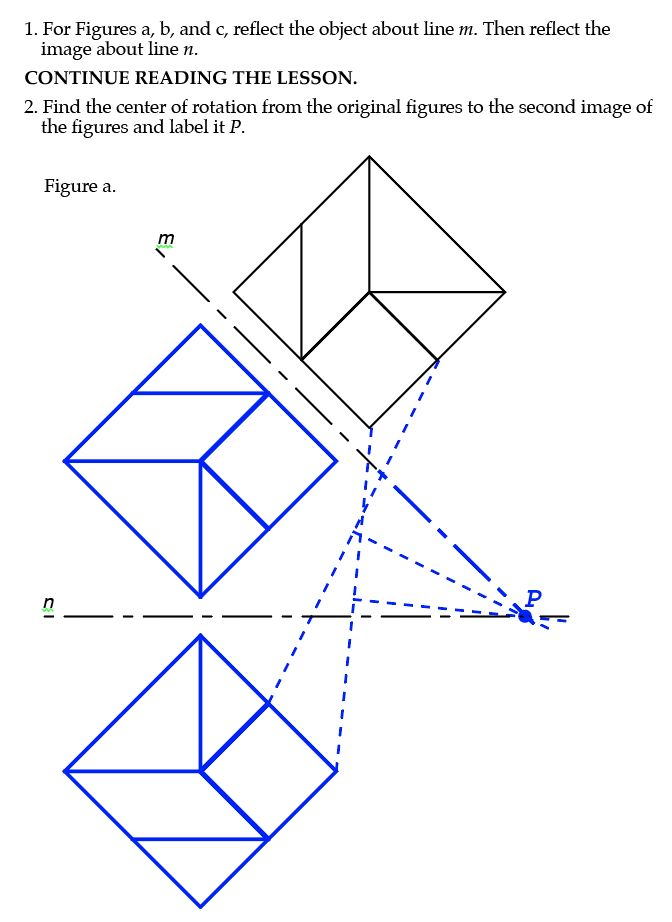
So let’s look at the graph, problem a. What is the angle between lines m and n? Extend line m to intersect line n. Using your handy-dandy goniometer, you’ll see it’s 45º. Write that down.
So what’s the angle of rotation of the top figure that’s been reflected and reflected? That’s the trickier part. I find it helpful to label a point or two on the original figure, then find the same points on the two new figures and label them accordingly. Personally, I chose the “bottom” of the “diamond,” the bottom of the original figure, AND the furthest point to the right. Label the same points on the new figures. Now it’s easier to see the answer. So how much did it rotate? 90º.
But wait. Before you dance off to the second problem, let’s double check if the rotation is clockwise or counterclockwise. The lesson says that if the rotation is counterclockwise, the rotation is positive. So what is this one? Going from the top image given to the second image drawn, it’s counterclockwise. Therefore, it’s positive. Which is what we had written.
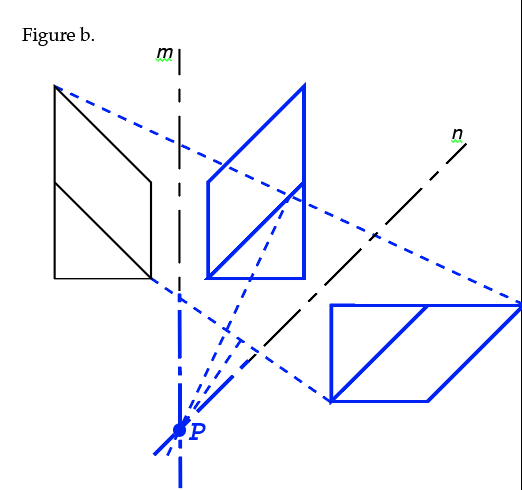
Then, if needed, find points to label and identify in the original figure and the new figures. How are these rotated? 90º again. Positive or negative 90º? Well, was it clockwise or counterclockwise? Right again – clockwise. So it’s -90º!!
I told the student that I’d let them tackle the rest of the chart. I received an email a few days later saying “I was able to complete my math by myself.” Way to go!
