Can you believe that it’s already time for my second to last post of the summer? And I have saved the best game for it. Yeah, yeah, yeah – I know that every week we tell you that the game is fun. Well, this is genuinely the most fun of all the fun games. It was our favourite game of the last school year and it had Robbie and me laughing until we couldn’t see straight.
And guess what? It’s not even in the Math Card Games book! Yup, I bet you didn’t know that RightStart™ has a few games that aren’t in the games book. This one is called Make Twenty and it’s found exclusively in the RightStart Math Level F Lessons book. It’s about making expressions, so it’s good for a student who is getting ready for algebra. As you play, you’ll get lots of practice with the order of operations and with using different strategies to manipulate numbers.
This game doesn’t take much to set up. All you need is the deck of basic number cards and a handful of tally sticks. If you want your student to have practice recording expressions, you can also grab a pencil and a page from the math journal – or any other paper you have lying around.

If you’re playing with just two people, you’ll only need about half the deck of basic number cards; if you’re playing with more, feel free to use the whole deck. Shuffle the cards, and deal four cards to each player.
In this game, your goal is to use some or all of the cards in your hand to make an expression that equals 20. You’ll be turning and arranging cards in different ways to show different operations. Here are all the strategies at your disposal:
Cards laid side by side mean addition.

9 + 2
Turning a card sideways means that it’s being subtracted.

9 – 2
Crossing the cards like an x means multiplication.

9 × 2
Placing one card below the other means that you’re dividing; it will look like the “fraction form” of division.

9/2
Placing one card slightly above and to the right of another indicates an exponent.

9²
You can even overlap cards to make double-digit numbers if you like.

92
And finally, you can use the tally sticks as parentheses.

9 × 2 × (9 – 2), which is the same as 18 × 7
We don’t often pull out the tally sticks, because there are usually ways of arranging an expression so that parentheses aren’t necessary. But they are available if you need them; and if your student is still learning the order of operations, they will come in handy.
Now that you’ve got an understanding of all the ways you can manipulate your cards, I bet you’re eager to get going and create some expressions!
So let’s play. Robbie is my opponent for this game. He goes first (because somehow in this family, the kid always goes first when we play), and after some thought he lays this down:

9 + 7 + 4 = 20
He copies down the expression in his math journal:
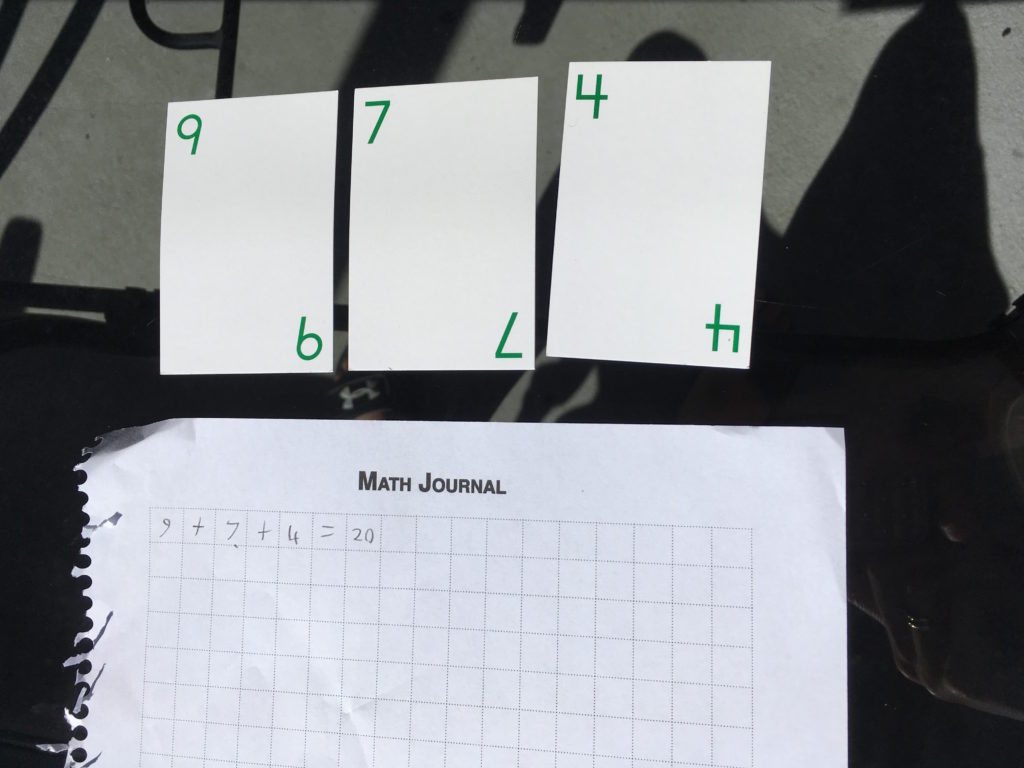
and then he picks up three new cards so that he again has four cards in his hand. The three cards that he used to make the expression go into his “winnings” pile. Now it’s my turn.
This is my hand:

Do you see anything I can do? I have to think about it for a minute, but soon I realize that I can make 20 with three of the cards. Here’s my solution:
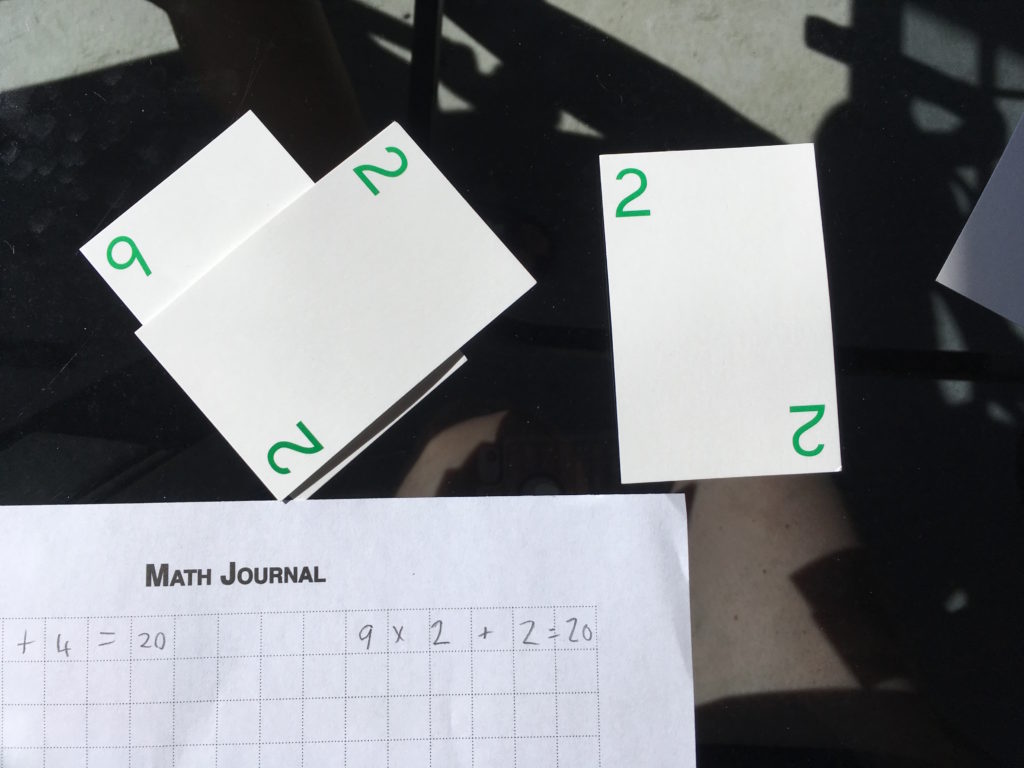
9 × 2 + 2 = 20
After writing out the expression, I gather the cards and place them in my “winnings” pile, and draw three more cards.
Sometimes, you won’t be able to think of a way to make 20 using the four cards in your hand. When this happens, you can discard any two cards in your hand and pick up two new cards. That’s what happens to Robbie on his next turn. He skips his turn, and it’s my turn again.
I still have the 4 in my hand from last time, plus I’ve picked up a 1, 6, and 8. Here’s what I came up with:
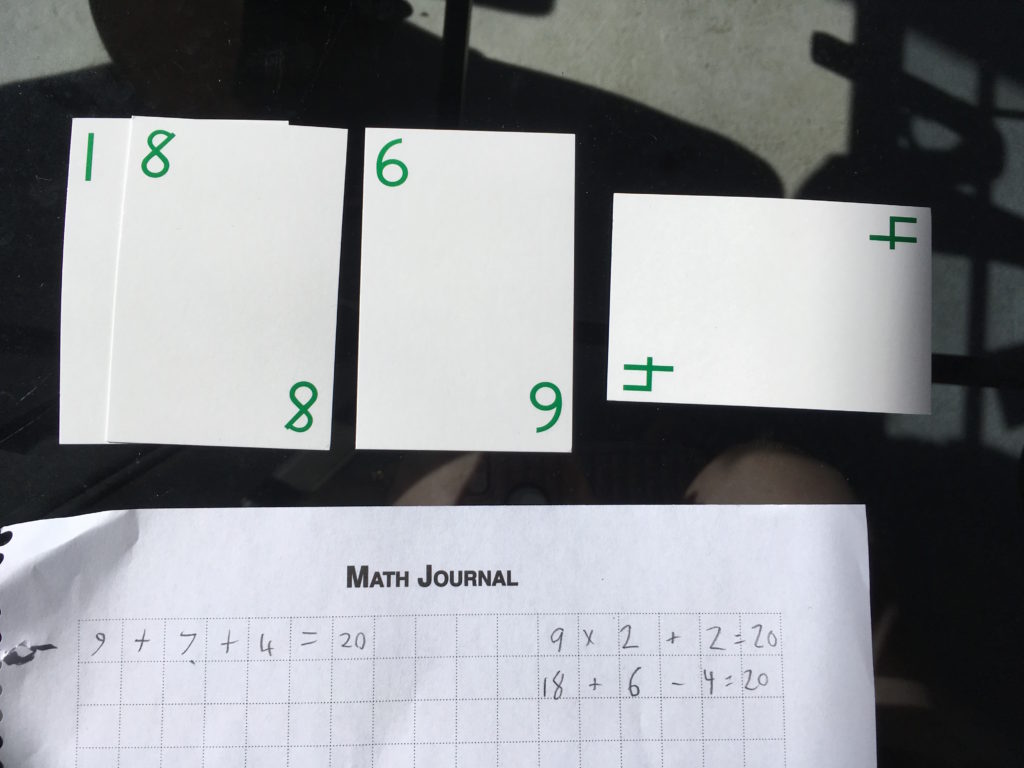
18 + 6 – 4 = 20
Those four cards are added to my winnings pile, and I draw four new cards.
Are you getting the hang of it? That’s about all there is to this game. We keep playing until the card stock is exhausted; and whoever has the most cards in their winnings pile at the end wins the game.
We love Make Twenty, but one of its drawbacks is that it can go pretty slow. It’s a problem-solving game, and like any good problem-solving game, it requires a measure of deep, careful, deliberate thought. It may be a while before you see a way to make 20 with the cards in your hand. And if you have stubborn players, they may not know when to give up! For example, here’s one of my hands.

I stared at this for what felt like an hour and I could not think of a way to make 20 using these numbers. Please help me out! Do you see anything I could have done?
As it happens, Robbie and I are both stubborn players. So after we played this game a couple times, we came up with a few variations to help it move a bit more quickly.
But… you don’t get to see them today, because this blog post is getting too long. You’ll have to wait until next week’s post. That’s when I’ll show you how to modify the game to make it easier or more challenging, and I’ll also show you the variation that had us laughing until we couldn’t see straight.
In the meantime, give this game a try and let us know what you think. And of course – tell me if you can find a solution to that hand that had me stumped! See you next week with the variations!

Loved this game Beth! Can’t wait for next week!
Such a fun game!
Fun game!
How about (9+1)x(8-6)?
This reminds me a bit of Number Knockout which my 10year old and I have come to love.
I knew someone out there would be able to do it! Thank you!
I hadn’t heard of Number Knockout and just looked it up – it looks pretty neat. Thanks for sharing.
(9+1)x(8-6)
Thanks Jane – I should have offered a prize for this – but at least you tie with Kirstin for bragging rights!!
You could have used all four of your cards 9,2,4,2: 9 x 2 + (4 – 2) = 20. That matters, since the winner of the game (as described in Level F, Lesson 15) is the one with the most cards used.
Ahhh….well that would have been a smarter move!