Multiplication has been the mathematical downfall of many children (and adults!). It’s not so much the problem of the algorithms, but rather it’s the problem of the memorization of the 100 facts.
Before expecting the child to learn the facts, we need to teach the meaning of multiplication. So often, we say it is the same as repeated addition. Yet describing multiplication as repeated addition provides a limited view. And it simply doesn’t work for multiplying fractions or decimals.
Since a primary application of multiplication is finding area, an array or an arrangement of objects in rows and columns makes a better model. A row with six objects repeated three times is 6 multiplied by 3, or as Montessorians say “Six taken three times.” This array produces a product of 18.

There are different interpretations about the meaning of 6 × 3. Sometimes 6 × 3 is thought of as 6 groups of 3, rather than 6 repeated 3 times. Let’s compare the meaning of multiplication to other arithmetic operations:
- When we add 6 + 3, we start with 6 and transform it by adding 3 to it.
- When we subtract 6 – 3, we start with 6 and transform it by decreasing 3.
- When we divide 6 ÷ 3, we start with 6 and transform it by dividing it into either 3 groups or groups of 3.
Therefore, to be consistent, when we multiply 6 × 3, we start with 6 and transform it by duplicating it 3 times.
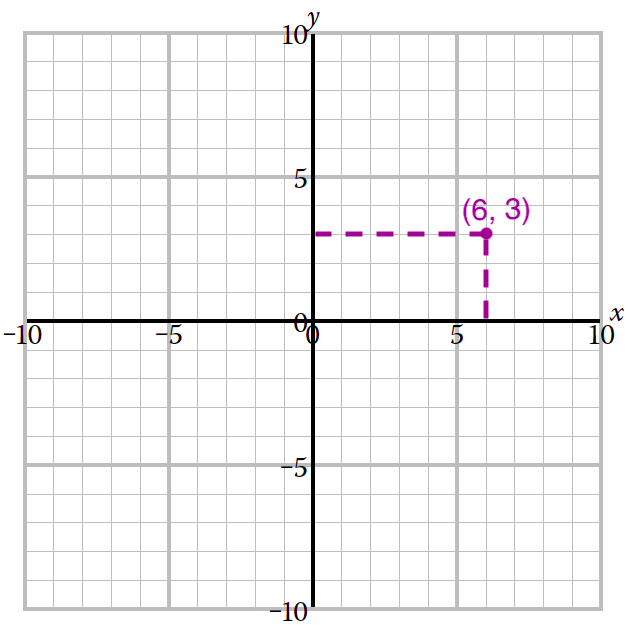
Note how this interpretation also corresponds to the Cartesian coordinate system. Representing the 6 × 3 array with 6 across in 3 rows is similar to finding a point (6, 3) on a grid. The first number, 6, indicates the horizontal number and the 3, the vertical number.
Missteps when Teaching the Multiplication Facts
All too often the multiplication facts are taught by rote, an overwhelming task, especially when 6 and 3 was previously learned as 9, but now it’s 18. Later, it will be 2, but that’s another problem….
Some programs increase the burden by extending the number of facts to be learned from 10 × 10 to 12 × 12. The 11s and 12s are not basic facts and increase the amount to be memorized by a whopping 44%!
The 11s and 12s can easily be figured out by adding 10 times the factor plus 1 or 2 times the factor. For example, 12 × 3 is 10 × 3 plus 2 × 3, which is 30 + 6, or 36.
Sometimes children learn their multiplication facts with songs or rhymes. One drawback is that the child needs to sing the song from the beginning until the needed fact is reached.
A second drawback to songs or rhymes to know the facts is the additional time the brain needs to transfer the information from the language section of the brain to the math section.
A third faulty approach to learning the facts incorporates pictures, one for each fact. For instance, to remember 4 × 4, one image shows a 4-wheel drive truck with the caption that the driver needs to be 16 to drive it.
When I first saw this, the legal age to drive in North Dakota was 14. Does that mean 4 × 4 is equal to 14? Or New Jersey where the legal age to drive is 17, so 4 × 4 is equal to 17 there?? And never mind Indiana where the legal age to drive is 16 and 3 months, or 16.25….
Seriously, these types of pictures cause a delay in fact retrieval because time is needed to translate unrelated pictures into mathematical concepts.
Another misstep is that the product obtained by multiplication is always greater than either factor. While it is true that 5 × 6 = 30 and the product of 30 is greater than 5 and 6, consider 7 × 1. The product of 7 × 1 is 7, but 7 is equal to the factor. It is not greater than 7.
Look at what happens when multiplying by zero: 257 × 0 = 0. The product 0 is certainly not greater than 257.
Also, when multiplying proper fractions, like ½ × ½ = ¼, the results are always less than either fraction.
So, why teach a “rule” when it is not true all the time?
Finally, what about using skip counting for teaching the facts? Although it seems to make sense to teach the facts through skip counting, children often resort to counting on their fingers to find the desired fact. I saw this in a school in England where the children were becoming fast counters, but they were not mastering the facts. Skip counting simply becomes another rote procedure to overwhelm and frustrate the child.
Learning the Facts through Visualization
For learning the multiplication facts, there is nothing like the commutative property to simplify the task. I still think it’s amazing that 6 × 4 is equal to 4 × 6.
The commutative property reduces the number of facts to be learned in a 10 by 10 multiplication table from 100 facts to 55 facts.
Learning the 1s facts is easy.
- 1 × 8 means 1 repeated 8 times. Answer is 8.
- 8 × 1 means 8 taken 1 time, which also is 8.
The 2s facts are already known from the addition facts.
- 4 × 2 is the same as 4 + 4 and 9 × 2 is the same as 9 + 9.
- The commutative property extends to 2 × 4 = 8 and 2 × 9 = 18.
The 10s facts are known from place-value work.
- 10 × 3 is the same as 3-ten, which is 30. It can also be viewed at 10 three times, or 30.
Now there are only 28 facts to learn.
The Cotter Abacus provides great visualizable strategies. For example, enter 6 × 4 on the abacus. Remember, this means 6 duplicated 4 times.
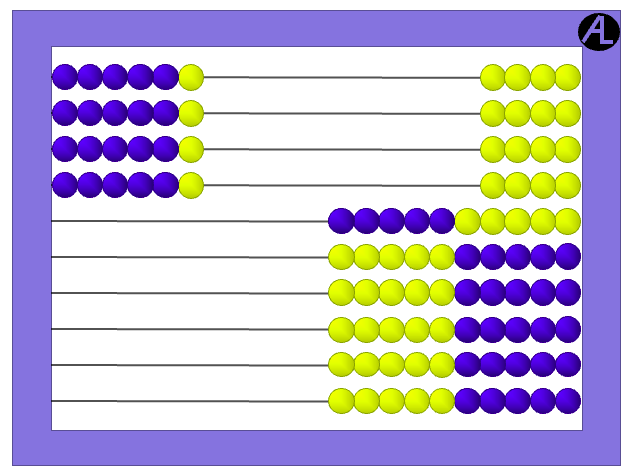
We generally think in pictures and children definitely think in pictures. This picture of 6 × 4 gives the child the picture of what 6 × 4 means and a way to find the product.
See the two groups of 10s? And the four ones? This makes 6 × 4 equal to 10 × 2 plus 4 more, which is 24.
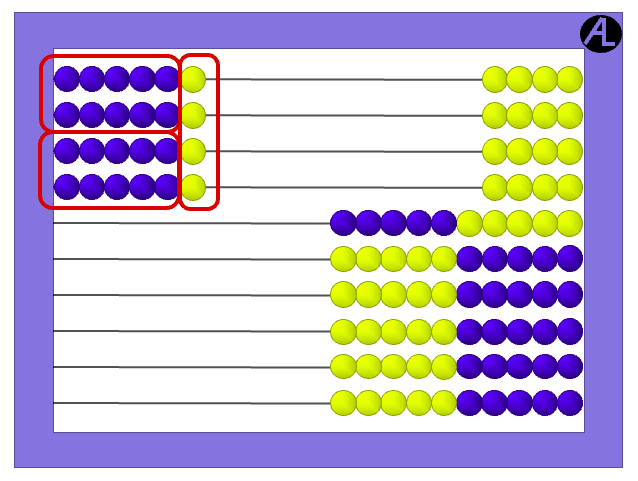
Another approach to 6 × 4 is thinking of 3 × 4, which is 12, and doubling that for a total of 24.
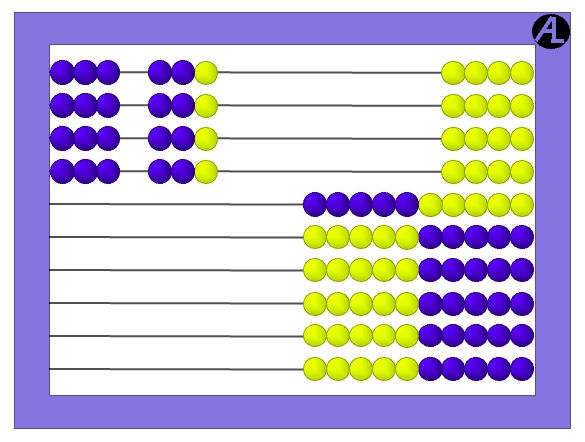
The fact 9 × 3 can be seen as 10 × 3, which is 30, less 3 that are not included to give 27.
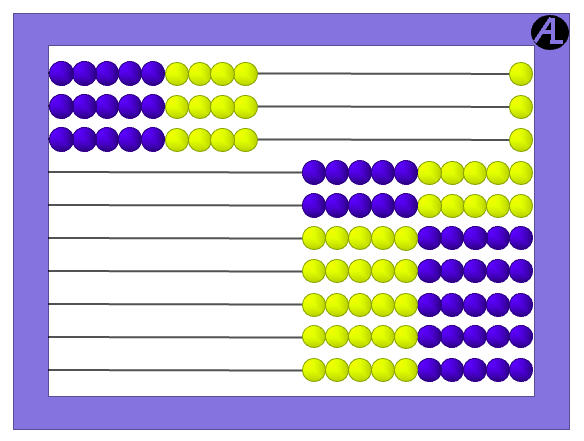
One last example is 7 × 7.
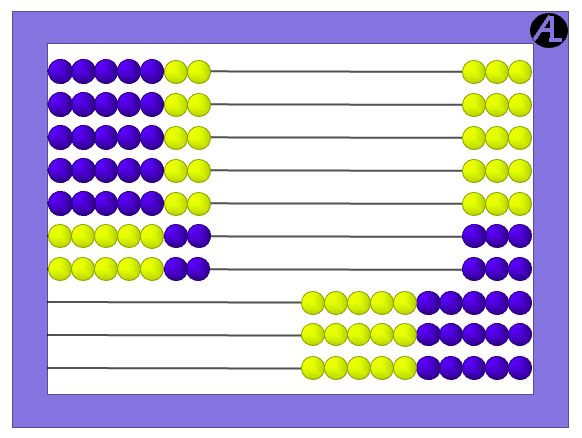
Here you can see the five rows of five blue beads that make 25. Also see a 10 yellow beads along the right two columns and another 10 in the bottom two rows. Finally, the lower right corner has 4 more.
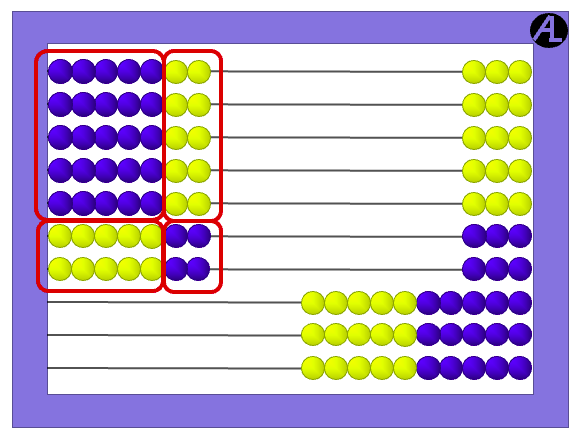
It takes less than 2 or 3 seconds to summon the visual image of 7 × 7 and find the product: 25 + 10 + 10 + 4 = 49.
Remember, a child is considered to know a fact when they can answer in 2 or 3 seconds.
All of the multiplication facts can be found on the Cotter Abacus. Allow your child to find the pattern that works for them.

And the cool thing in this view of multiplication, as is the case of 6 x 4; to develop the distributive property of multiplication:
(5 + 1) x 4 = 4 x 5 + 4 x 1 = 20 + 4 = 24.
I am loving this AL Abacus!
In 7 x 7:
(5 + 2) x (5 + 2) = 5 x 5 + 5 x 2 + 2 x 5 + 2 x 2 = 25 + 10 + 10 + 4 = 49.