Did you check out our blog on division? And did you read about short division? Isn’t that just wonderful? Now, let’s talk about some practice for short division.
When I was a child, my mother created puzzles for my siblings and me. They were called multivides. Multivides are a great self-checking activity that uses both multiplication and short division.
Multivide is a blend of the two words: multiplication and divide.
The best way to tell you about multivides is to do one together. Since this is a column of numbers, some children benefit from grid paper or lined paper turned to write a long column of numbers. This will help keep things organized.
Let’s start with a multivide for 2. Write 2 down at the top of the column. Then, multiply 2 by 3 vertically and write the product, 6.
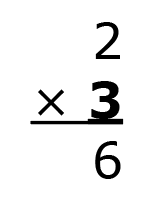
Next, multiply the product, 6, by 4, which is 24.
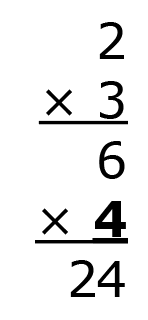
Continue by multiplying that product by 5, and the next product by 6.
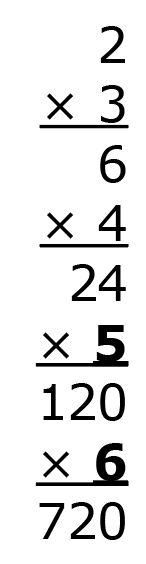
Now, for the next part of the multivide, we will divide by the same numbers, 3, 4, 5, and 6, in the same order. To continue building the column, we are going to use the division house upside down.
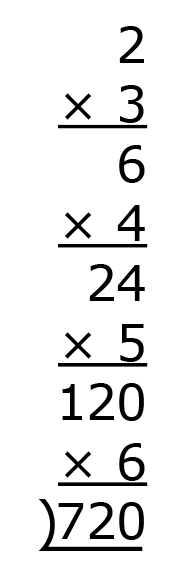
Find the quotient for 720 ÷ 3 and write it below the dividend.
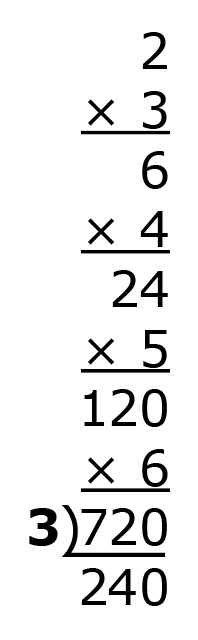
Then divide the next quotient by 4, then that quotient by 5, and finally, the last quotient by 6. The multivide is complete.
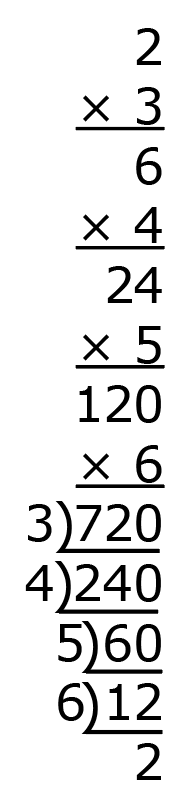
There should never be a remainder when doing a multivide. If you do have a remainder when dividing, it means you made a mistake somewhere and need to find and correct the error before going on.
What is the starting number of the multivide? What is the ending number? They are the same! Will that happen every time?
Another Multivide
Let’s try another multivide and see if the starting and ending numbers are the same. Start with 9, then multiply and divide by 5, 6, and 7, in that order.
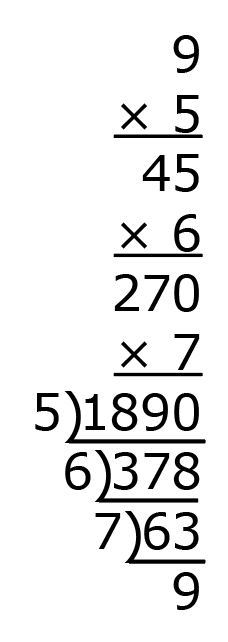
Is the ending number the same as the starting number? It is!
The multivides above are “partial” multivides. At this point, unless the student is curious, limit the multivides to three or four numbers to multiply by, and then divide by the same. Here is a video of Kathleen doing a partial multivide with some students.
Multivide Game
This game can be played as a solitaire game or as a multiplayer game. If two or more players are available, this creates an opportunity for everyone to work together and check their products and quotients with each other as they progress through the multivide. It is not a race, but rather, it is a time to collaborate and help each other.
Eight basic number cards are needed, one of each number 2 through 9. Each player will also need something to write on; grid paper is ideal.
Shuffle the eight cards well, then turn over the first card. Write that number on the top of the paper. Turn over the next card. If the second card drawn is an 8 or 9, put it at the bottom of the deck and redraw another card.
Multiply the number on the first card by the number on the second card to find the product. Next, increase the second card’s number by 1 and multiply the new product by this number. Then, add 1 again to the multiplier and find the product. Finally, divide the product by the same three numbers in the same order.
For example, if the first card is a 3 and the second card is a 7, multiply 3 by 7 for a product of 21. Next, 7 + 1 is 8, so multiply 21 by 8 for a product of 168. Then, 8 + 1 is 9, and 168 × 9 is 1512. Finally, divide 1512 by 7, which is 216, and continue the process.
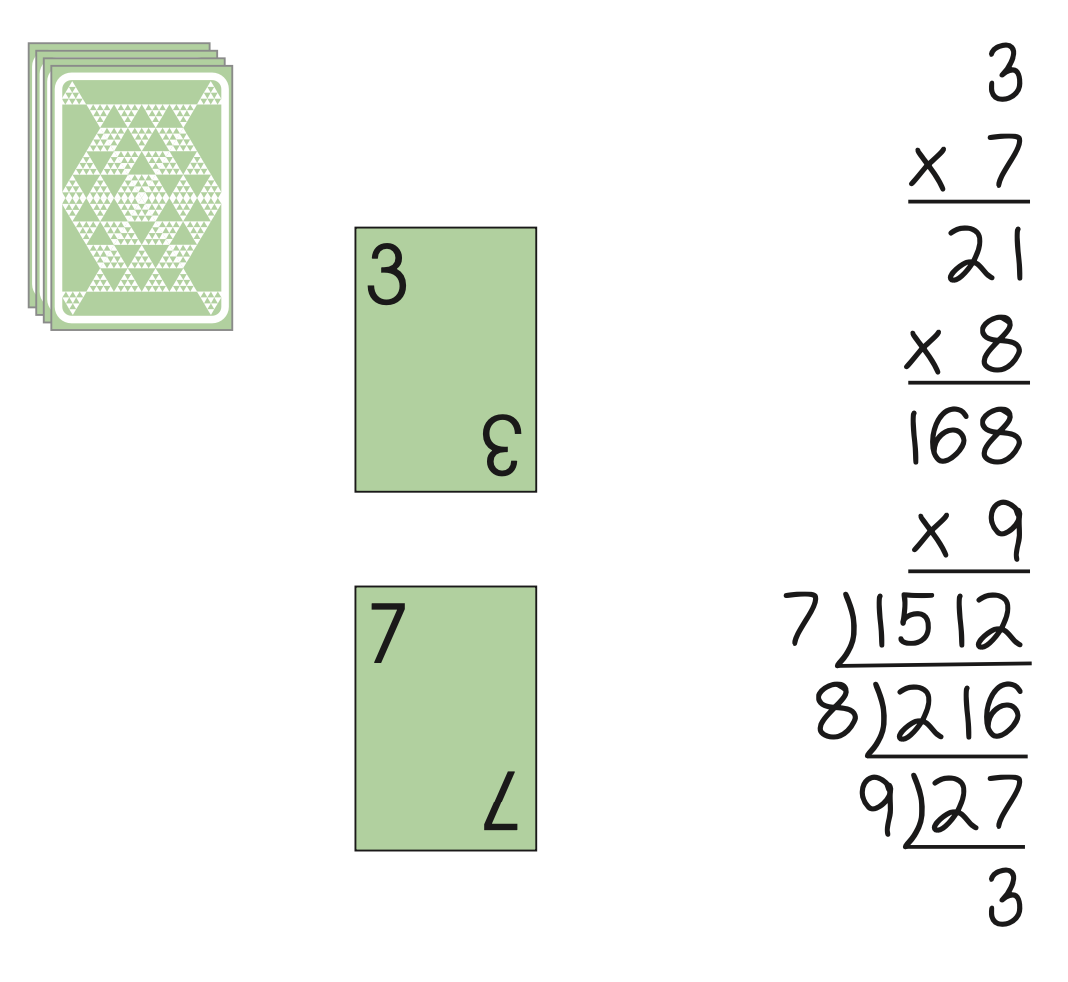
The round is won when the end number is the same as the starting number. Play at least two rounds.
Full Multivide
For the person who is interested in doing a full multivide, pick any number, multiply it by 2 through 9, then divided by 2 through 9.
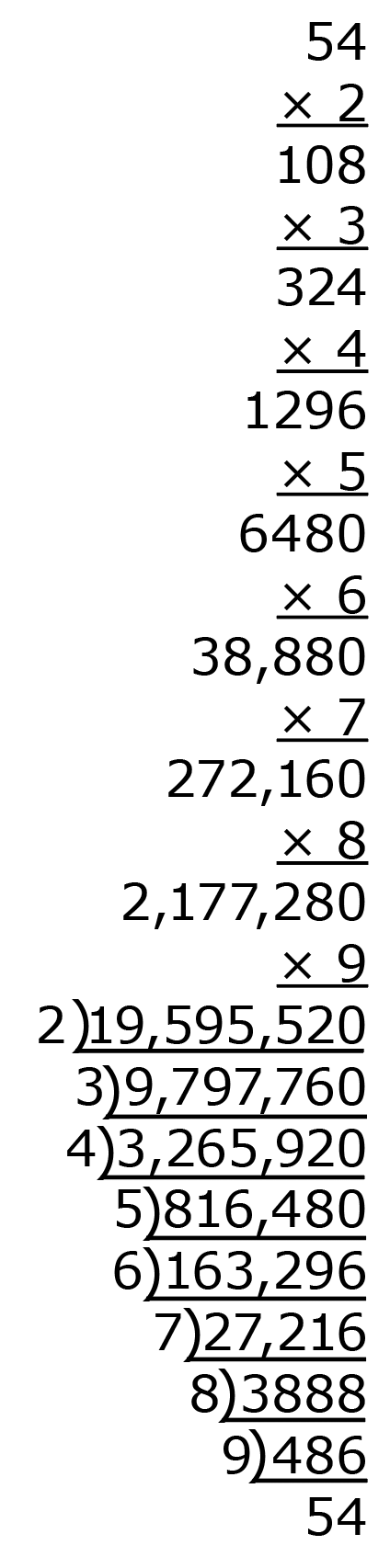
I hope you enjoy this as much as I do!
