Nicea called me for help with RightStart Mathematics Level H. She is homeschooled and is working through the program with some assistance from her mom, Julia, and a little assistance from me.
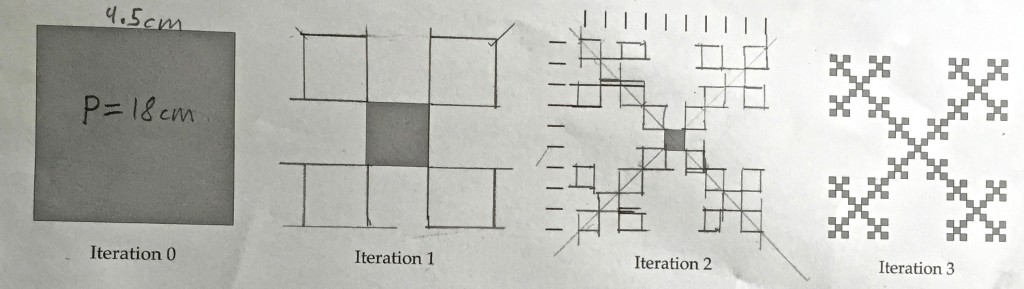
Today’s question was Lesson 30, Box Fractal, and Lesson 31, Box Fractal Perimeter and Area. The goals of these lessons is to learn about fractals. So, what IS a fractal? A fractal is a pattern which repeats itself at smaller and smaller scales, resulting in an irregular shape. Here’s what I’m talking about.
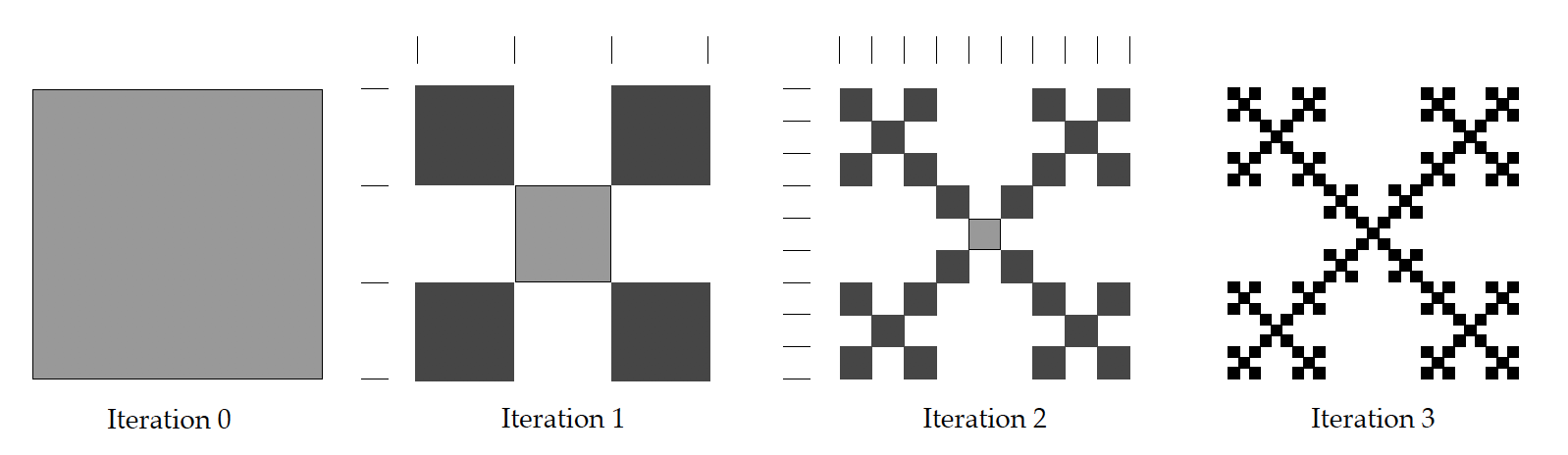
See how the first square, Iteration 0, is reduced in size, duplicated, then creates the same shape over and over? The worksheet asks the student to create these same fractals. Once that is done, there is an analysis of the iterations.
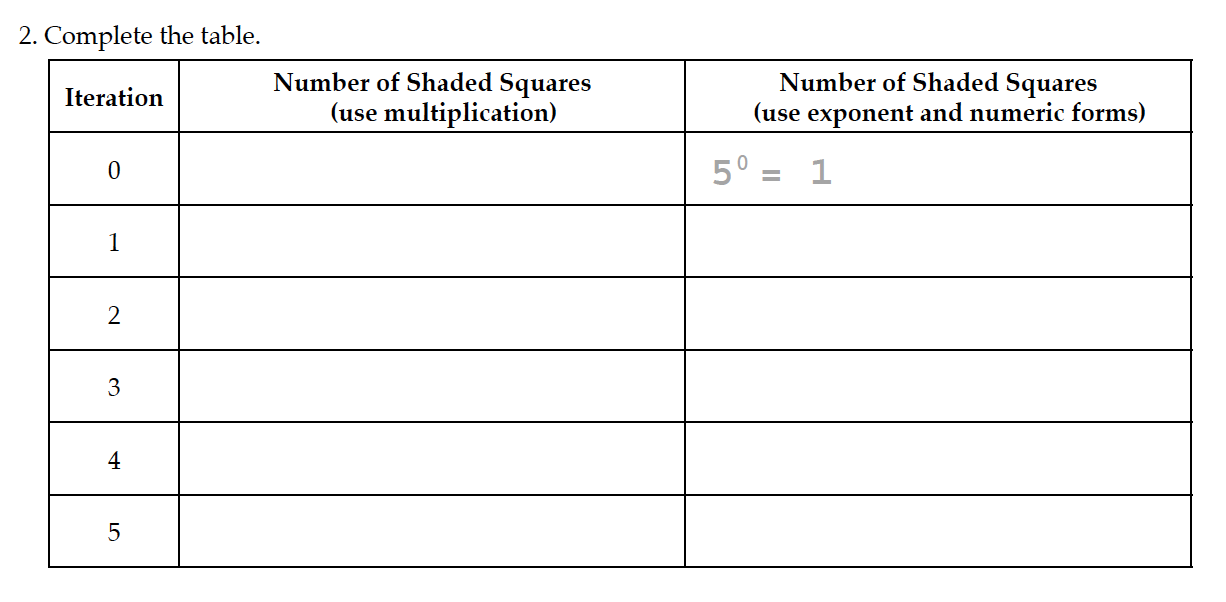
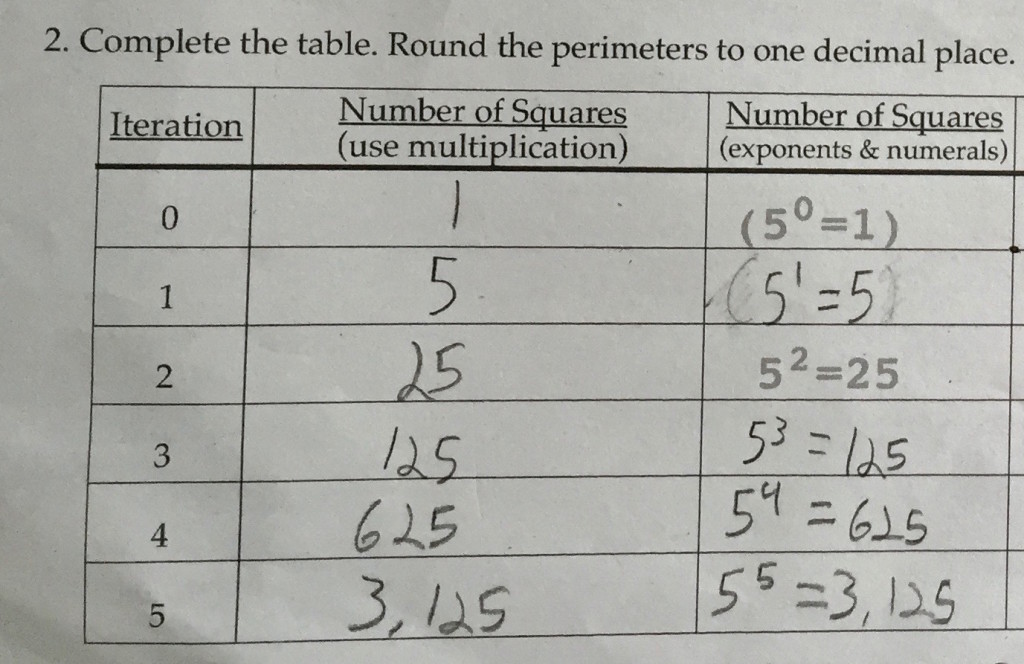
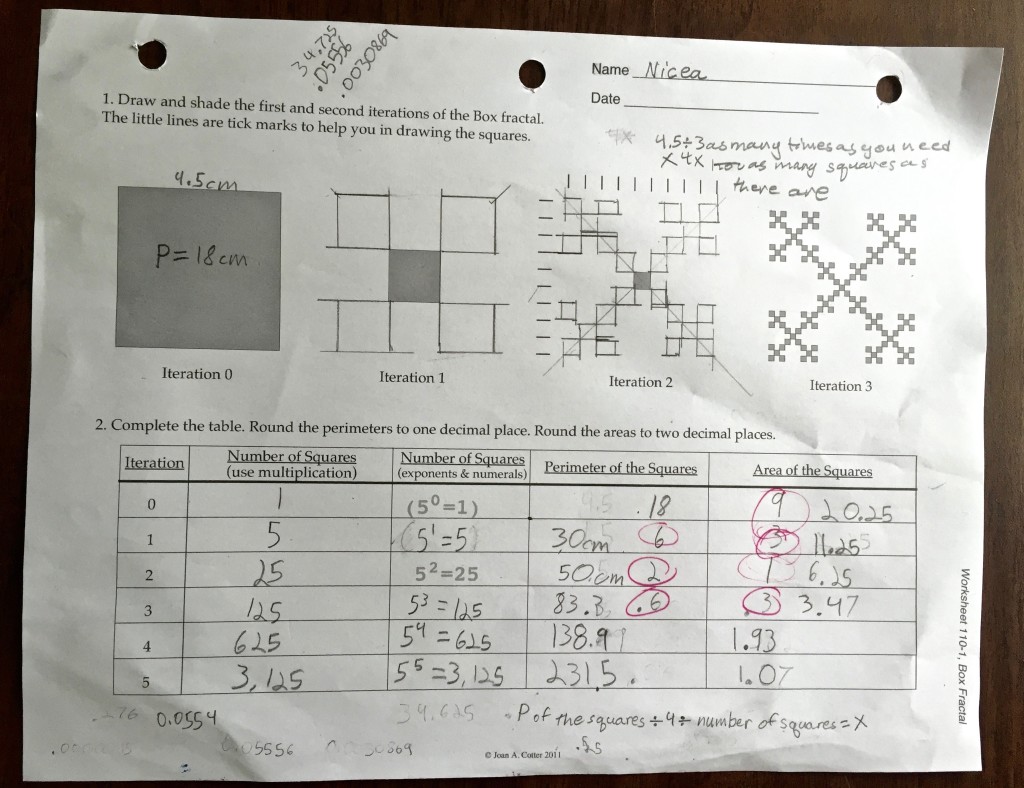
Let’s look at this one column at a time, ok? Number of squares in Iteration 0 is 1 square. That’s obvious. Iteration 1 is 5 squares. Pretty easy, right? Iteration 2 will be 5 × 5 which is 25 squares. Again, not too challenging. Iteration 3 will be 5 × 5 × 5. See how that works? That means we have 125 squares. Iteration 4 isn’t shown, but we have a pattern happening. So Iteration 4 will be 5 × 5 × 5 × 5 = 625 and Iteration 5 will be 5 × 5 × 5 × 5 × 5 = 3125.
By the way, let your students use their calculators here. In the real world, no one in their right mind would do these calculations long hand with paper and pencil! The calculator frees the student to experience the patterns and uses of multiplication without the burden (and possible inaccuracies) of mind-numbing paper and pencil work.
Now, let’s write these same calculations using exponents. Again, the pattern is very evident. Each iteration creates another square of our five box pattern. Nicea got these all correct without a problem.
The next lesson asks us to calculate the perimeter of the iterations.
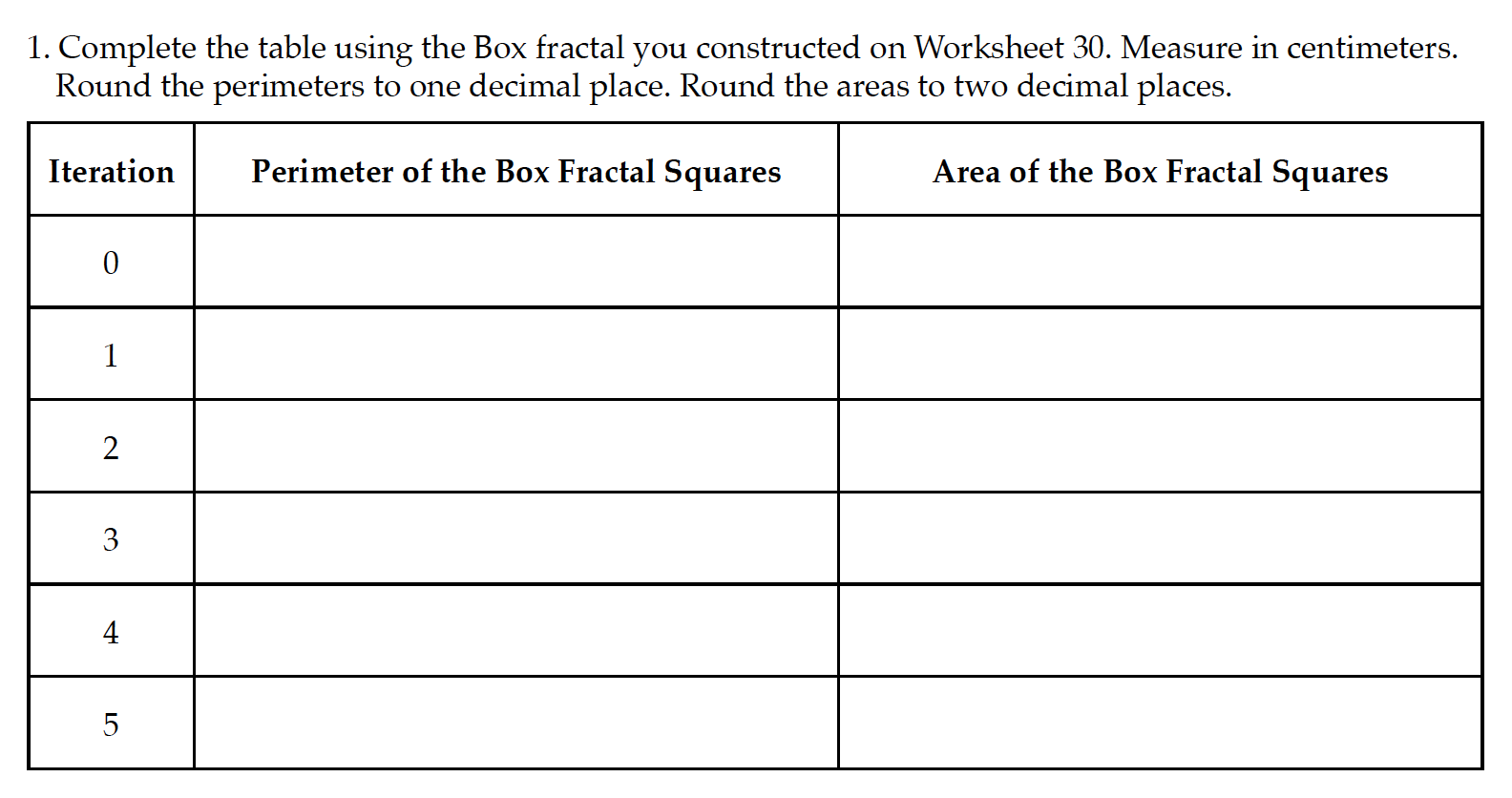
This seems a bit overwhelming and Nicea thought so too. Let’s step our way through the process. Also, remember that there was a pattern with the first two pieces of information we calculated. Think there might be one here too?
Perimeter of Iteration 0 means we need to measure the edge of our square. Nicea came up with 4.5 cm. So perimeter will be 4.5 × 4 which equals 18 cm. Easy.
For Iteration 1, Nicea measured the edges of the small square and came up with 1.5 cm. Then she took 1.5 × 4 to get the perimeter of one square, 6 cm. There was a little confusion on whether to measure one square or all the squares. But look at the heading. It reads “Perimeter of the Box Fractal Squares.” The plural “squares” would mean more than one, so we’re looking for the perimeter of all five squares. One square has a perimeter of 6 cm so she multiplied 6 cm by five squares and came up with 30 cm for the perimeter of Iteration 1.
Looking at the future iterations and the measurement precision that would be necessary, I considered the situation mathematically. I knew that one side of Iteration 0, the big square, was 4.5 cm. Since Iteration 1 was obviously breaking it into three pieces, I figured 4.5 ÷ 3 on my calculator and came up with 1.5. This is the measurement of one side of the square. Perimeter would then be 1.5 × 4 which is 6 cm. And since there’s five squares, 6 × 5 = 30 cm, same as what Nicea came up with.
Nicea approached Iteration 2 the same way she had before: she measured the tiny edge of one square and came up with .5 cm. She was right, but I suggested we approach it mathematically. After a bit of conversation, we ended up with 4.5 ÷ 3 ÷ 3 (for each iteration) = 0.5 cm. Taking that single side and calculating the perimeter of one square, she then multiplied that single square’s perimeter by the number of squares in Iteration 2 calculated previously, 25: 0.5 × 4 × 25 = 50 cm.
Following the same process, Nicea’s work looked like this.
Iteration 3: 4.5 ÷ 3 ÷ 3 ÷ 3 = 0.17 and 0.17 × 4 sides = 0.67 then 0.67 × 125 squares = 83.3 cm
Iteration 4: 4.5 ÷ 3 ÷ 3 ÷ 3 ÷ 3 = 0.06 and 0.06 × 4 sides = 0.22 then 0.22 × 625 squares = 138.9 cm
Iteration 5: 4.5 ÷ 3 ÷ 3 ÷ 3 ÷ 3 ÷ 3 = 0.02 and 0.02 × 4 sides = 0.07 then 0.07 × 3125 squares = 231.5 cm
And she is right. But that’s a lot of number punching on the old calculator! So how could we make this easier? How about if we build the next iteration based on the current one?
Going from Iteration 0 to Iteration 1, we took the edge measurement, divided by 3, multiplied by 4 to get the perimeter of one square, then multiplied by the 5 squares. So, what if, rather than take the edge measurement, we take the perimeter measurement of 18 cm, divide that by 3, then multiply by 5 squares: 18 ÷ 3 × 5 = 30 cm. Another way we could write it is 18 × 5 ÷ 3 or 18 × 5/3 = 30 cm.
Let’s apply our new method to recalculate the perimeters of the iterations.
Iteration 1: 18 (perimeter from iteration 0) × 5/3 = 30 cm
Iteration 2: 30 × 5/3 = 50 cm
Iteration 3: 50 × 5/3 = 83.3 cm
Iteration 4: 83.3 × 5/3 = 138.9 cm
Iteration 5: 138.9 × 5/3 = 231.5 cm
Well, that was a whole lot easier. And it’s exactly what we had with our long round about method!
The next thing we need to is find the area of each iteration. Iteration 0 is super easy: 4.5 × 4.5 = 20.25 cm². Of course, you could also just say 4.5² = 20.25 cm².




For the next iterations, Nicea approached this in a very unique way. Looking at Iteration 1: 30 cm (Iteration 1’s perimeter) ÷ 4 (to get one square’s side’s measurements) ÷ 5 (as the number of squares in Iteration 1) = 1.5 cm. Because we need the area, we square our answer, 1.5, and get 2.25 cm². Then 2.25 × 5 (as the number of squares in Iteration 1) = 11.25 cm². Correct!
Can this girl think or can she THINK?? I’m delighted to admit that she totally ran circles around me with her process!
Let’s draw all the iterations out, using Nicea’s methodology:
Iteration 1: 30 ÷ 4 ÷ 5 = 1.5 cm then 1.5² = 2.25 and 2.25 × 5 = 11.25 cm²
Iteration 2: 50 ÷ 4 ÷ 25 = 0.5 cm then 0.5² = 0.25 and 0.25 × 25 = 6.25 cm²
Iteration 3: 83.3 ÷ 4 ÷ 125 = 0.1666 cm then 0.1666² = 0.02775556 and 0.02775556 × 125 = 3.47 cm²
Iteration 4: 138.9 ÷ 4 ÷ 625 = 0.05556 cm then 0.05556² = 0.00308691 and 0.00308691 × 625 = 1.93 cm²
Iteration 5: 231.5 ÷ 4 ÷ 3125 = 0.01852 cm then 0.01852² = 0.00034299 and 0.00034299 × 3125 = 1.07 cm²

See her notes? She is accurate, but a lot of number crunching. I wonder if there’s an easier method again….
Let’s look at the area of Iteration 0 to Iteration 1.




We’ve taken Iteration 0, the big square with a calculated area of 20.25 cm², and, for Iteration 1, divided it into nine squares, and only want to know the area of five of the squares. In other words, we are taking 20.25 ÷ 9 × 5 = 11.25 cm². Let’s rearrange equation and make it look like this: 20.25 × 5 ÷ 9. Or this: 20.25 × 5/9.
Will that work for all the iterations? Let’s check it out…..
Iteration 0: 4.5² = 20.25 cm²
Iteration 1: 20.25 × 5/9 = 11.25 cm²
Iteration 2: 11.25 × 5/9 = 6.25 cm²
Iteration 3: 6.25 × 5/9 = 3.47 cm²
Iteration 4: 3.47 × 5/9 = 1.93 cm²
Iteration 5: 1.93 × 5/9 = 1.07 cm²
It DOES work! So that, my friends, is how you figure the perimeter and area of this particular fractal. If you or your child has another method, please let us know!
