When teaching math to a child, there are three important questions to consider:
- Are manipulatives necessary for teaching math?
- What is the purpose of manipulatives?
- Are some manipulatives better than others?
First of all, let’s define manipulatives. A concrete manipulative is a physical object that a child handles in order to learn mathematics. Some math programs use no concrete manipulatives. Others use them only as a last resort when a child has difficulty understanding a concept. Still others, like RightStart Mathematics, use manipulatives as a teaching tool.
A good concrete manipulative is one that a child will internalize, so that it becomes available for the child to use mentally.
RightStart manipulatives include the Cotter Abacus, overlapping place-value cards, fraction charts, base-10 picture cards, and centimeter cubes. Research shows that it takes at least a year for a child to obtain the full benefit of a manipulative.
Some of the materials children use during math class such as rulers, geoboards, calculators, and goniometers (angle measurers), are not actually manipulatives, but rather are math tools.
Applications of math are a third type of manipulative. These include clocks, coins, and math card games.
In the nineteenth century, many American schools had some beautiful geometric models, in both two and three dimensions. The teacher usually used these for demonstrations or as a prop during explanations.
Montessori preschool classrooms have a set of geometry solids for the children to handle. RightStart includes a geometric set where the children explore properties, learn the names, make comparisons, find their weights, and calculate their surface areas and volumes.
According to researchers, two important outcomes of using manipulatives are children increase their learning and have a more positive attitude towards math.
Manipulatives need to be incorporated into the lesson and not used as a reward. Therefore, there should be no distinction between “real” math and “fun” math.
Some might argue that ordinary objects found around the home can become manipulatives. They suggest that using familiar objects makes math seem more “real.” This might be true for some simple concepts. However, using raisins or other goodies makes it hard for a child to think about math topics and not the tempting treat. Additionally, common objects often need to be modified to be mathematical, which can be challenging. Finally, using these everyday objects makes it harder to see the math concept being learned because math is abstract.
Keep in mind that one purpose of education is to expand the child’s horizons beyond their familiar environment. This makes it necessary to use specially designed materials, such as the fraction chart which includes all fractions from halves to tenths.
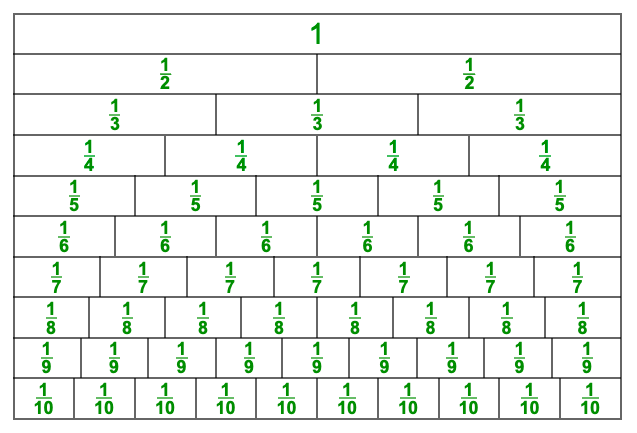
The field of mathematics is doubling every seven years. Therefore, it is impossible to find everyday objects to explore these more advanced concepts.
One common manipulative are colored rods that vary in length, usually from 1 cm to 10 cm, with each length having a specific color.
To use colored rods mathematically, you must first memorize the color for each of the ten numbers. Then to add 4 + 3, you need to find the 4-rod, the yellow rod, and the 3-rod, the pink rod.
Lay them end-to-end and find their sum by locating the third rod, the tan rod, that matches the length of the two rods and translating that color into a number.
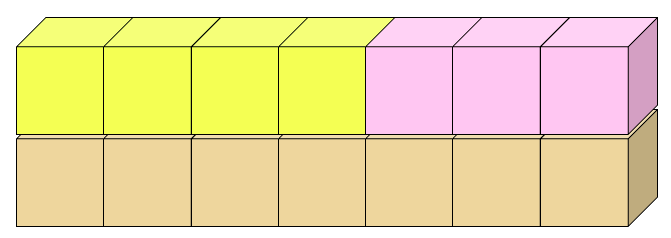
Also keep in mind that the colors are a problem for 8% of boys who are color deficient.
A serious drawback of colored rods longer than five is that they are not visualizable. Can you see what the quantity is without counting?
Very few people can see a quantity of eight mentally and be confident it is eight. This makes it impossible to work with colored rods mentally. Curricula using colored rods usually rely on flash cards to ensure that children learn the facts.
Rather than colored rods, RightStart uses the Cotter Abacus. This abacus has rows of beads grouped in fives to make the quantities visualizable. To add 4 + 3, 4 beads are entered followed by 3 beads.
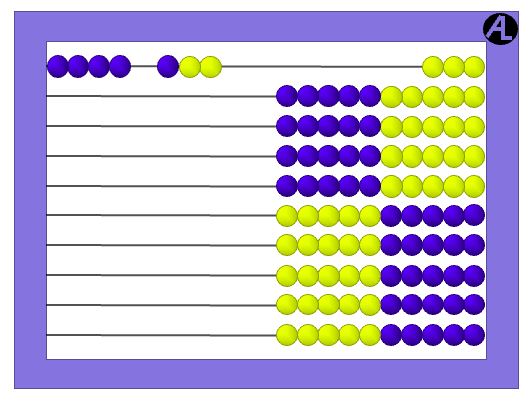
The sum is seen immediately as 5 and 2, or 7. This amount is visualizable.
Another common manipulative are sets of base-10 blocks, which is shown as a single cube for 1s, ten cubes arranged a bar for 10s, ten bars arranged as a square for 100s, and stacks of ten squares arranged as a large cube for 1000s.
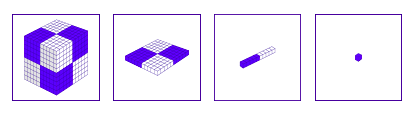
Notice how the quantities of the base-10 are also grouped in fives to make the quantities visualizable.
With this material, it is possible to represent any whole number from 1 to 9999.
To understand how the base-10 blocks represents our number system, children must recognize a ten, a hundred, and a thousand each as new units. Failure to recognize ten as a new unit is thought to be the result of too much counting, especially beyond ten.
Working with manipulatives does not guarantee understanding the mathematical concept. The teacher must ensure that the child understands the mathematics embedded in the materials.
Manipulatives are needed, but they must be chosen carefully. They must be more than simple counting items. Teachers need to guide the children toward understanding and making the concepts visualizable.
