Place value is the very foundation of arithmetic. Place value packages numbers into groups of tens and tens of tens. This makes calculating large numbers similar to adding single-digit numbers: 3 + 4 is similar to 30 + 40, 300 + 400, 3000 + 4000, and so on.
We need to regard place value as a wondrous gift.
Instead of giving our children a seemingly endless string of number words as recited with the counting sequence, place value allows us to neatly group our numbers and to work with them efficiently.
Place value was considered so important in the fifteenth century that the first printed arithmetic textbook, Treviso Arithmetic of 1478, states that there are five fundamental operations: numeration (place value), addition, subtraction, multiplication, and division. Interestingly, the word “place value” didn’t even make it into the dictionary until 1911.

Sadly, place value seems to be a difficult concept for many children and even adults. Because Western children are traditionally taught to add by counting and counting ignores place value, thinking in terms of tens and ones becomes a burden when counting.
Children in Eastern Asian countries do not experience difficulty learning place value because those languages are transparent in number naming. For example, eleven is ten-1, twelve is ten-2, and sixteen is ten-6. This contrasts with English teen numbers where the ones and the tens are reversed and the word for ten has morphed into teen, as in sixteen. Also, twenty-one is 2-ten 1, and twenty-three is 2-ten 3. Here the word for ten is morphed into -ty.
Children who learn to name numbers with transparent words tend to use strategies based on tens. They make tens whenever possible. Consider the Cotter Abacus when adding 9 + 5. Enter 9 on the first row and 5 on the next row.
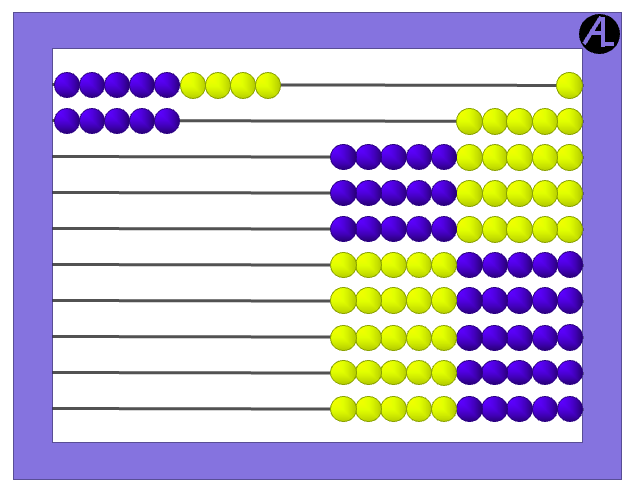
Using the Complete the Ten Strategy, take 1 from the 5 to make the 9 into a 10.
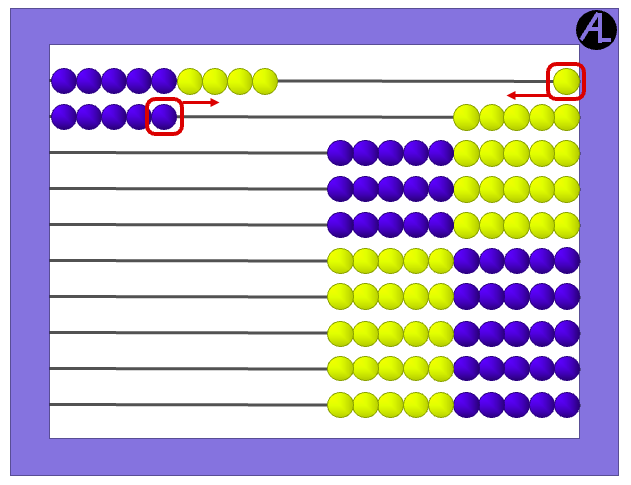
Then this shows the sum of 9 + 5 as 10 + 4, which is 14.
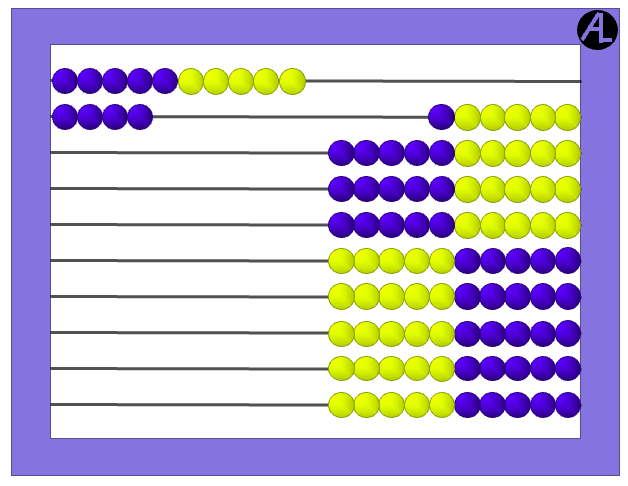
Unfortunately, many English-speaking first graders do not know 14 as 10 and 4 more. They see 14 as simply part of a sequence: …8, 9, 10, 11, 12, 13, 14…
Is there anything we can do about this? Yes!
We can teach children to refer temporarily to the numbers from 11 to 99 by their transparent number names.
My research shows that children using these transparent number names gain the same benefits as the native Asian speakers. With transparent names, the sum of 10 and 4 is obviously ten-4.
Next, give the children two groups of tens and tell them it is called 2-ten.
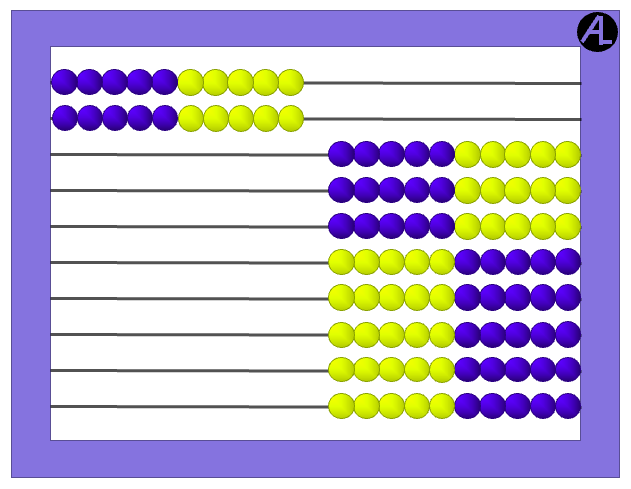
This is repeated for three groups of tens, 3-ten, up to nine groups of tens, 9-ten.
They are also given place-value cards printed with: 20, 30, . . . 90. Point to the 2 while saying two and point to the 0 while saying ten. The zero changes 2 into 2-ten.
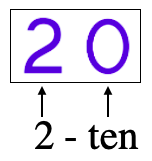
Continuing on with ten groups of ten, we show the children the place-value card of 100. Ask them to point out how it says 10-ten. The first two digits show ten and the last zero says it’s ten.
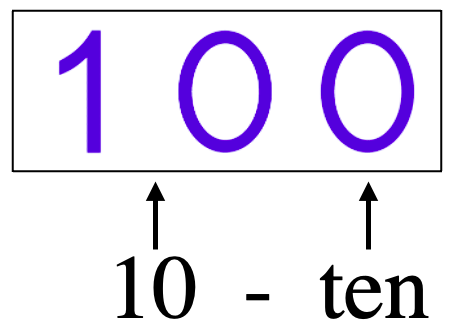
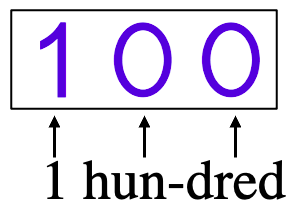
Next, we tell them it has another name, one hundred. Point to the 1 while saying one, then point to the first zero while saying “hun,” and point to the last zero while saying “dred.”
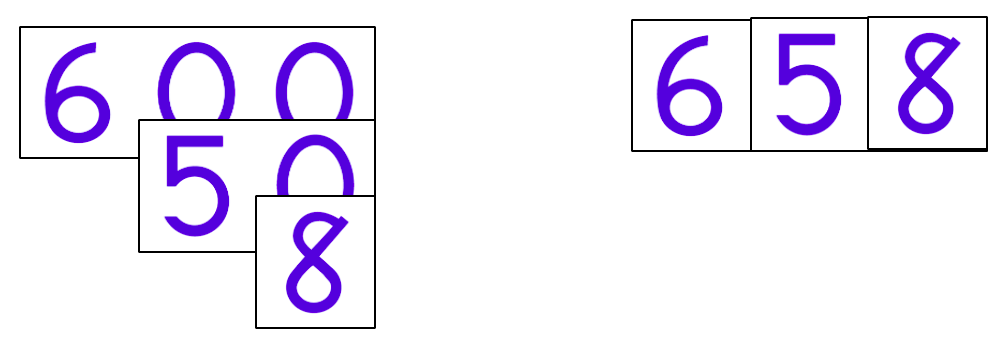
When combining numbers with different place values, the corresponding cards are stacked. The cards are stacked by length with the longest card on the bottom and edges aligned on the right. Thus, cards for 600, 50, and 8 when stacked show 658.
Here are place value cards for 200 and 7 stack to show 207. Notice any unneeded zeros are hidden, but necessary zeros are visible.

Place-value cards encourage reading numbers beginning at the left. The child first states the digit, notes how many digits follow, and then states the correct place value word.
Reading numbers starting from the left matches the way we say numbers and it matches the direction we read.
Unfortunately, the traditional method of reading the numbers starts at the right and identifies column headings to decide the place value of the leftmost digit.
Then, transition from the transparent number names to the traditional names by saying 4-ten has another name, forty, with the “ty” meaning ten. Repeat for 60, 70, 80, and 90.
The numbers 30 and 50 have a variation in pronouncing the three and five syllable of the word, which is also found in thirteen and fifteen.
The number twenty enunciates the “w,” like twelve, twin, and twice, although the “w” is silent in two.
The teen names from 13 to 19 are said in reverse order with “teen” meaning ten.
This leaves 11 and 12 as mysteries. Centuries ago people decided the call the number 11, a one left, because it was one left over ten. However, they reversed the one left and called it a left one, which eventually became eleven.
Twelve evolved from two left, with the “w” of two pronounced. Mystery solved.
Sometimes people think children can understand place value better if the ones, tens, and hundreds are color-coded. Unfortunately, 8 percent of boys are color deficient, so color coding is not helpful. Also, children relying on color schemes may view numbers having “color value” rather than place value.
Instead of giving our children a seemingly endless string of counting words, start by introducing transparent number names to allow them to group their numbers, to build an understanding, and to work with algorithms efficiently.
