Luke gave me call for help with RightStart Mathematics Level H. He was on Lesson 32 and confused on the formula for finding the perimeter of iterations of a fractal.
Huh, you say? Well, Lesson 32 discusses Koch Snowflake, a very famous fractal. The basic pattern is an equilateral triangle. Here’s what they look like.

Iteration 0 and 1, the first two in the line up above, were given to Luke on the worksheet, so he drew Iteration 2 using the triangle grid paper. Here’s a peek.
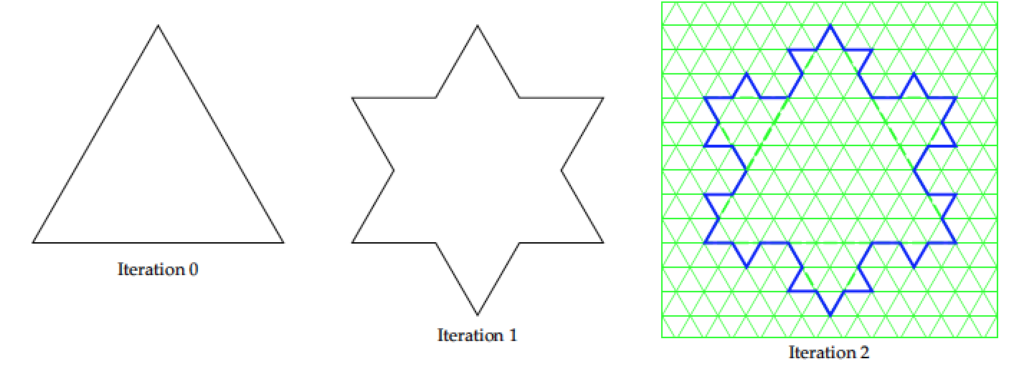
That was easy, right Luke?
Now, the hard part. How do we figure out the perimeter? The lesson says, “Rather than measure the perimeter in centimeters, use the edge of a small equilateral triangle on the grid paper.”
Look at the pink triangle, Iteration 0, outlined on the graph paper here. Ignore the blue shape. See how there are 9 small green equilateral triangles per side? Since there are three sides to a triangle, and 9 × 3 is 27, the perimeter of Iteration 0, the pink equilateral triangle below, is 27.
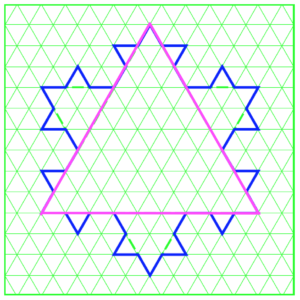
Easy peasy lemon squeezy.
Now let’s look at the perimeter of Iteration 1. See how it added triangles onto the sides of the basic triangle? So what’s the perimeter now? Sure, you could count all the way around, and, provided you counted accurately, you’d come up with 36. But you know this isn’t the most effective or efficient method, right? So let’s look at this mathematically.
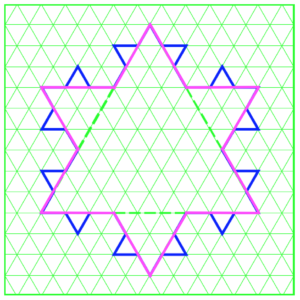
You could break it down and say that each side of the six pointed shape, 12 segments altogether, measures 3 small triangles per segment. 12 × 3 is 36. That’s what we had when we counted. But still, there’s got to be an easier way, right?
Let’s start with just one side of the shape. Iteration 0 had one straight line all across, shown in pink, solid and dashed, line segments below. Iteration 1 added a triangle, shown in solid pink and black lines.
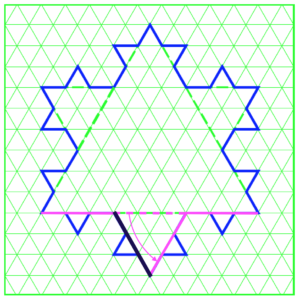
We know that straight line (solid and dashed pink segments) is 9 units long. Break it into three segments; 3 × 3. To make the solid line (pink and black) of Iteration 1, we’re keeping two of the three segment as is, then “moving” the middle segment (pink dashed) to the side of the new triangle, and adding a fourth (black) line. So let’s take the 9, divide it by 3, then multiply it by 4. That gives us 12. Since there are 3 sides like this, 12 × 3 is 36. Which is what we had when we counted it out.
So wouldn’t it make sense to just take the total perimeter of Iteration 0, which we know is 27, and divide that by 3, then multiply it by 4? We have 36 again!
OK, now what’s a faster way to write “divide by 3, and multiply by 4”? If I say it as “multiply by 4 and divide by 3”, does that give you a clue? What about “× 4/3”? What is 27 × 4/3? It’s 36!!
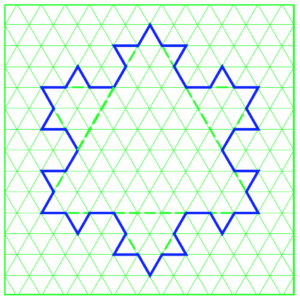
Let’s double check if this works for Iteration 2, the blue shape below. Now, we know that Iteration 1’s perimeter is 36. Calculating 36 × 4/3 gives us 48. And there you have the perimeter of Iteration 2! If you don’t believe me, have fun counting it out.
So, one last thing that Luke and I both missed. In the Level H Lesson book, look at the paragraph titled “Analysis” on page 55. It look like this.

What does that last sentence say? It reads “…each new side is four thirds as long as the original side.” Yikes!! Well, I guess Luke and I now understand WHY each new side is 4/3 of the original side! And we both need to brush up on our reading skills…..
P.S. RS2 Level H, Lesson 30 and Lesson 31 lays a great foundation for this lesson.
