Today we’re going to talk about why we teach multiplication to our younger children. Earlier this week I talked with Jenna from Portland. She was wondering why we’re teaching multiplication at this level. Very good question, Jenna!
We introduce multiplication in RS2 Level A in Lesson 59 and in RS2 Level B in Lesson 119. Why so early? Aren’t the children still working on addition? Yes, they are, but exposing them to multiplication earlier helps them see the connection between addition and multiplication. We use multiplication in everyday life, so let’s help the children see the usefulness and practicality of it.
Consider bringing treats to a party. If we want everyone to have two cookies and there are eight people, how many cookies do we need? 8 × 2 = 16. That’s multiplication. Yes, you could see it as an addition problem, 8 + 8, but the link to multiplication is right there. So we’re going to help the child experience that connection and application.
Multiplication is taught as arrays first. A what? An array is an arrangement in rows and columns. Let’s see what multiplication as an array looks like.
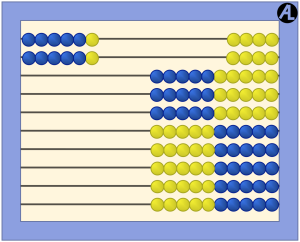
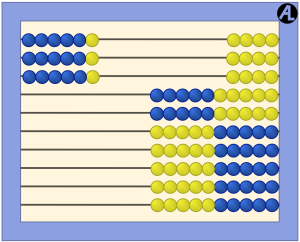
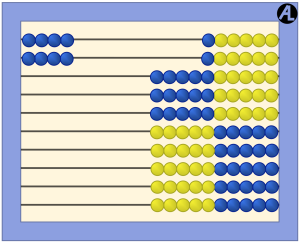
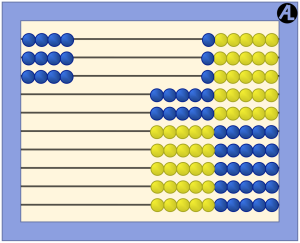
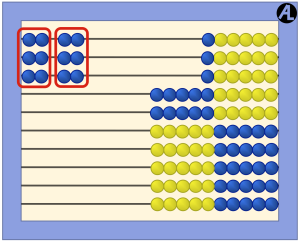
Enter 6 on the first wire of the AL Abacus. Now do it again. How much is it? 12. You can see the 10 with the blue beads and 2 with the yellow beads. So 6 taken 2 times is 12.
Clear the abacus. Now enter 6 on the first wire and then triple it. How many times did you enter 6? Three. How much is entered? 18. You can see the 15 blue beads and 3 more yellow beads. This equation is 6 taken 3 times equals 18 or 6 × 3 = 18.
What does 6 × 3 mean? Is it “6 taken 3 times” or is it “6 groups of 3?” As you can see above, we teach it as 6 taken 3 times. Consider the other arithmetic scenarios.
6 + 3: we start with 6 and transform it by adding 3.
6 – 3: we start with 6 and transform it by subtracting 3.
6 ÷ 3: we start with 6 and transform it by dividing 6 into 3 groups or into groups of 3.
Therefore, to be consistent, 6 × 3 starts with 6 and is transformed by taking it 3 times!
In the arrays shown above on the abacus, 6 represents the horizontal quantity entered on the first wire and 3 represents the vertical quantity, or the number of times 6 is entered. This is also consistent with the coordinate system; in (6, 3), the first number, 6, indicates the horizontal number and 3, the vertical number.
Let’s look at another array. Enter 4 × 2. Pretty easy to see the answer of 8. The answer is called the product.
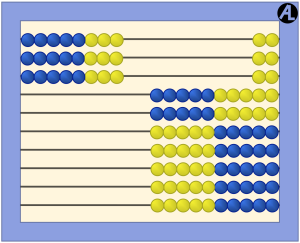
Enter 4 × 3. This one’s a little harder to see the total.
Split the 4s into two groups of 2s. Now you can see 2 × 3 = 6 and six doubled is 12; 4 × 3 = 12.
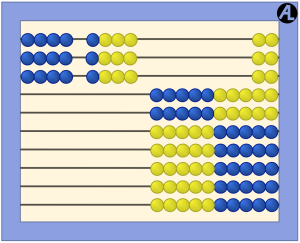
Look at 8 × 3. Again, the answer isn’t that easy to see….
….until you split the 8s into two groups of 4s. We know that 4 × 3 = 12 and 12 doubled is 24! So 8 × 3 = 24.
So why do we go through all the trouble to show the arrays for the multiplication facts? Why not just simply memorize and be done with it? So often mnemonics are used to “help” with the memorization process. Mnemonics are a story or rhyme used to assist remembering something. A well-known example is Roy G. Biv, the mnemonic for the sequence of rainbow colors: red, orange, yellow, green, blue, indigo and violet.
Generally, when using mnemonics for math facts, the facts are taught individually and often without a math perspective. The relationships between the facts are missing. For example, the mnemonics might be a 16-year-old getting their driver’s license so they can drive a 4×4 vehicle. This then reminds us that 4 × 4 = 16. Well, in South Dakota, children can get their license at age 14. So does that mean that 4 × 4 = 14 in South Dakota? And in New Jersey, 4 × 4 = 17? And how does 4 × 4 relate to 4 × 5? It’s just another “story” to remember, rather than 16 plus 4 more or 2 × 5 doubled is 20.
We want our children to understand! When a fact is simply memorized and not understood, it’s like reciting a poem or phrase in another language without knowing what the words mean. Sure, it might be recited perfectly, but if there’s no understanding, what’s the use? Deep and true learning requires understanding of the relationships in and around the learned information. And that’s why we start our younger children in multiplication sooner than later. Thanks for the question, Jenna!