Dr. Cotter on Addition and Subtraction Facts

Addition 

Addition can be thought of as finding the whole when the parts are known. Place value greatly simplifies finding the sum of two numbers. To be efficient in adding, we start with the sums of numbers 1 + 1 through 9 + 9. These are best learned through strategies, especially visualizable strategies, and through frequent usage. 

First, the children need to be able to recognize quantities grouped into fives, like our fingers. After they know the quantities, then they can begin to add numbers together using strategies.

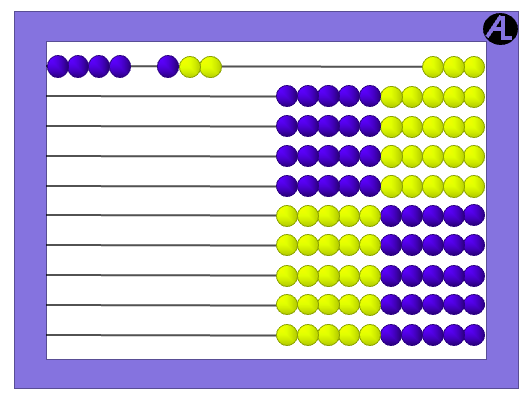
The strategies are first practiced with concrete objects in groups of fives and then imagined mentally. For example, to add 4 + 3, imagine a group of 4 objects and another group of 3 objects.

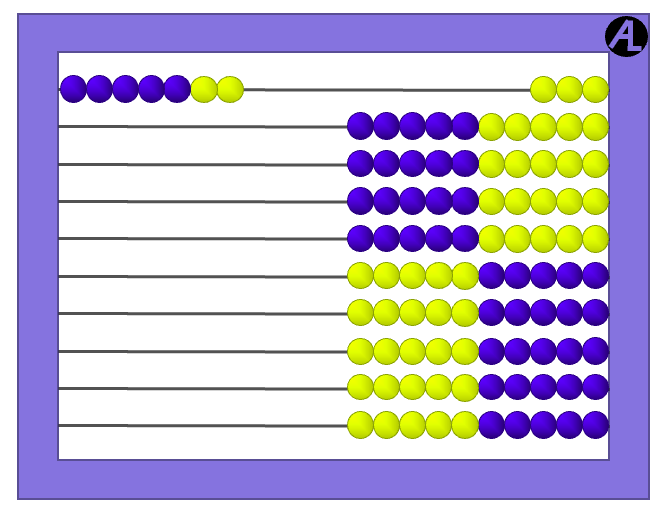
Next, mentally take 1 object from the 3 and give it to the 4, transforming the sum into 5 and 2, which is recognized as 7.

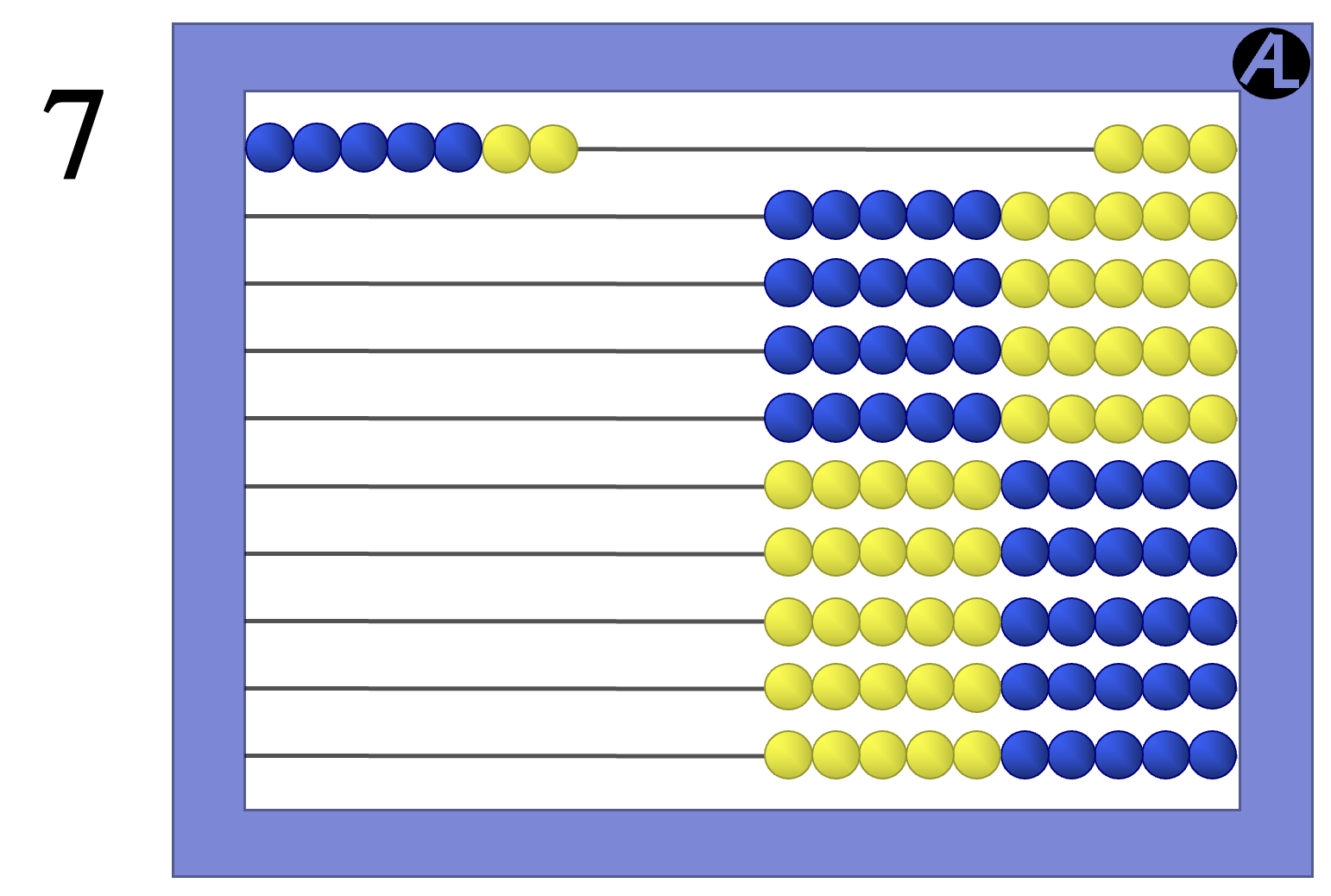
To add 7 + 3, think 7 is 5 and 2 and the 2 combined with 3 makes another 5. So the sum is 10.

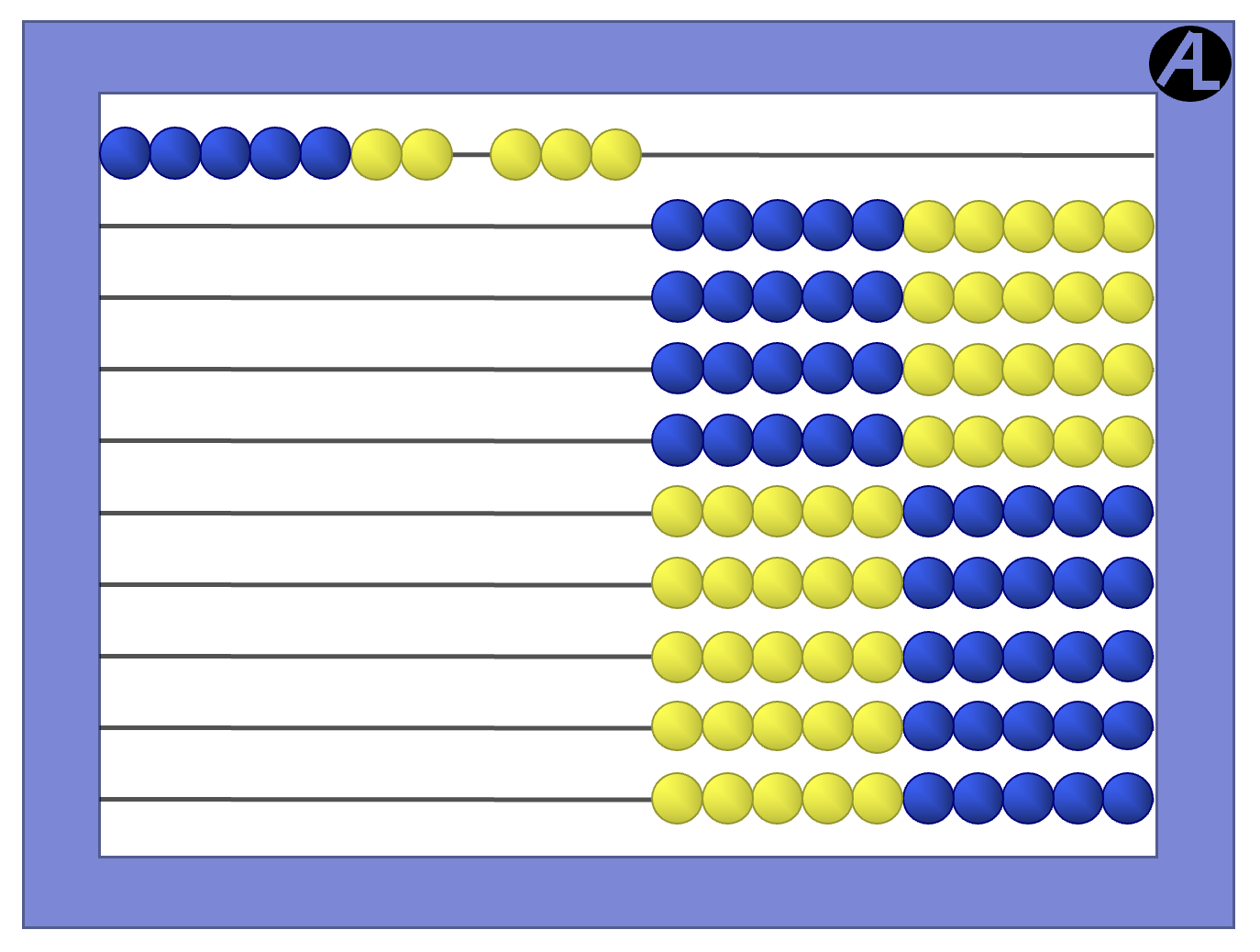
Writing this operation in equation form looks like: 

7 + 3 = (5 + 2) + 3
7 + 3 = 5 + (2 + 3)
7 + 3 = 5 + 5 = 10

Although this equation looks complicated, performing the process with objects is very quick and efficient. There is no point in having the children write these equations, rather this becomes a mental shuffle of quantities, resulting in a confident response.

A great strategy for larger sums is the Two Fives Strategy. Let’s add 7 + 6.

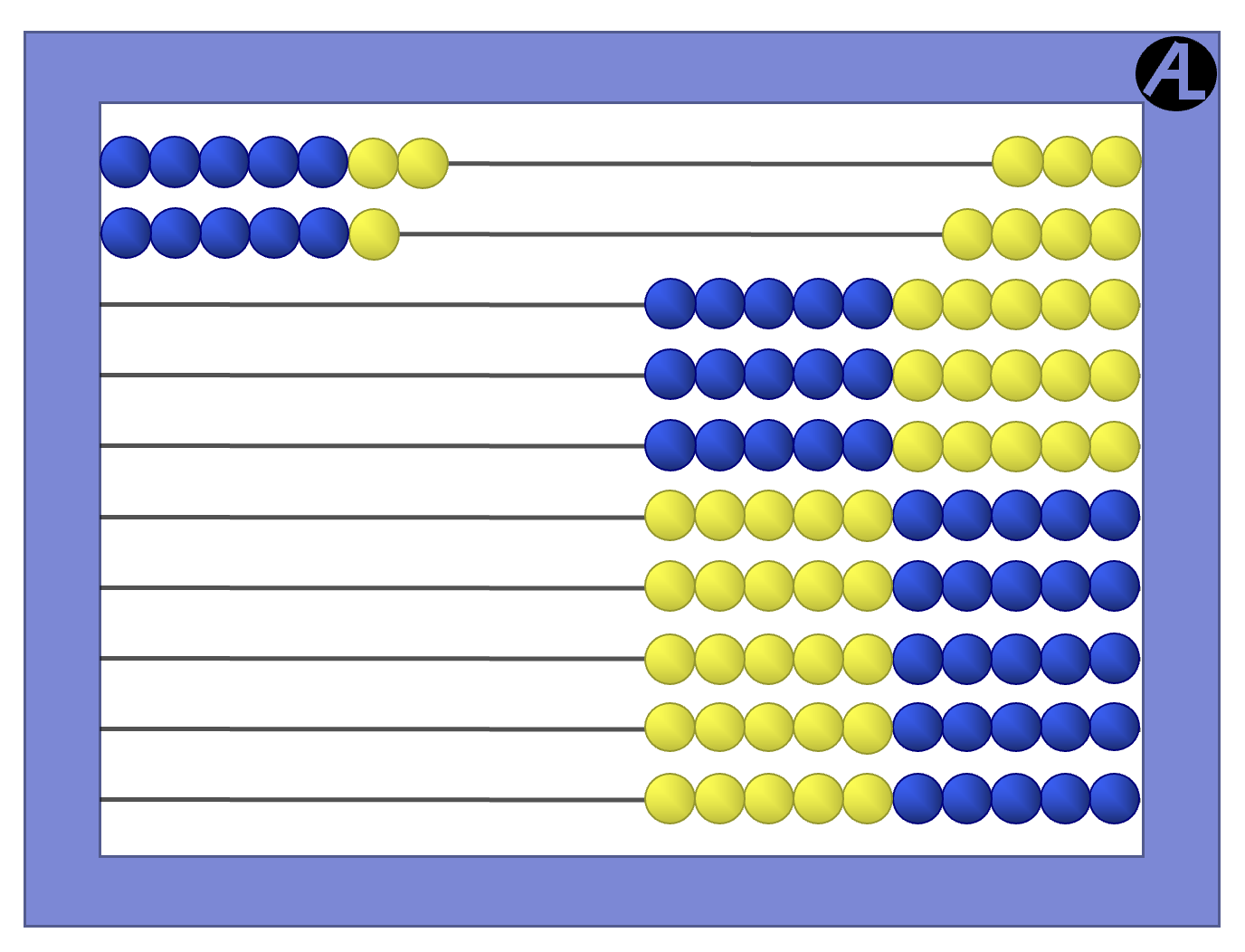
See 7 as a group of five and two more? And see 6 as a group of five and one more?

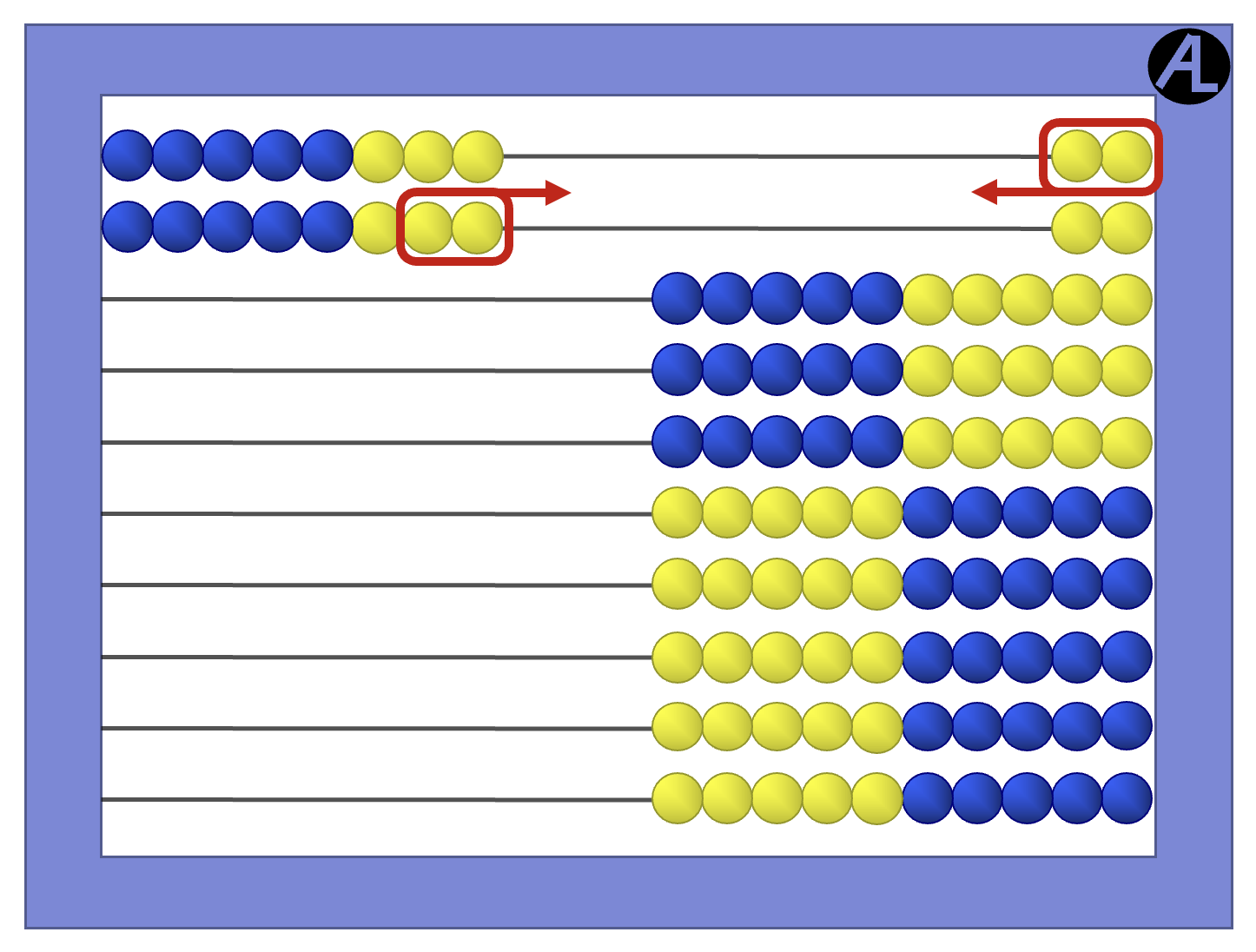
Combine the two groups of 5 to make ten and the leftover 2 and 1 to make 3, giving the sum of 10 + 3, or 13.

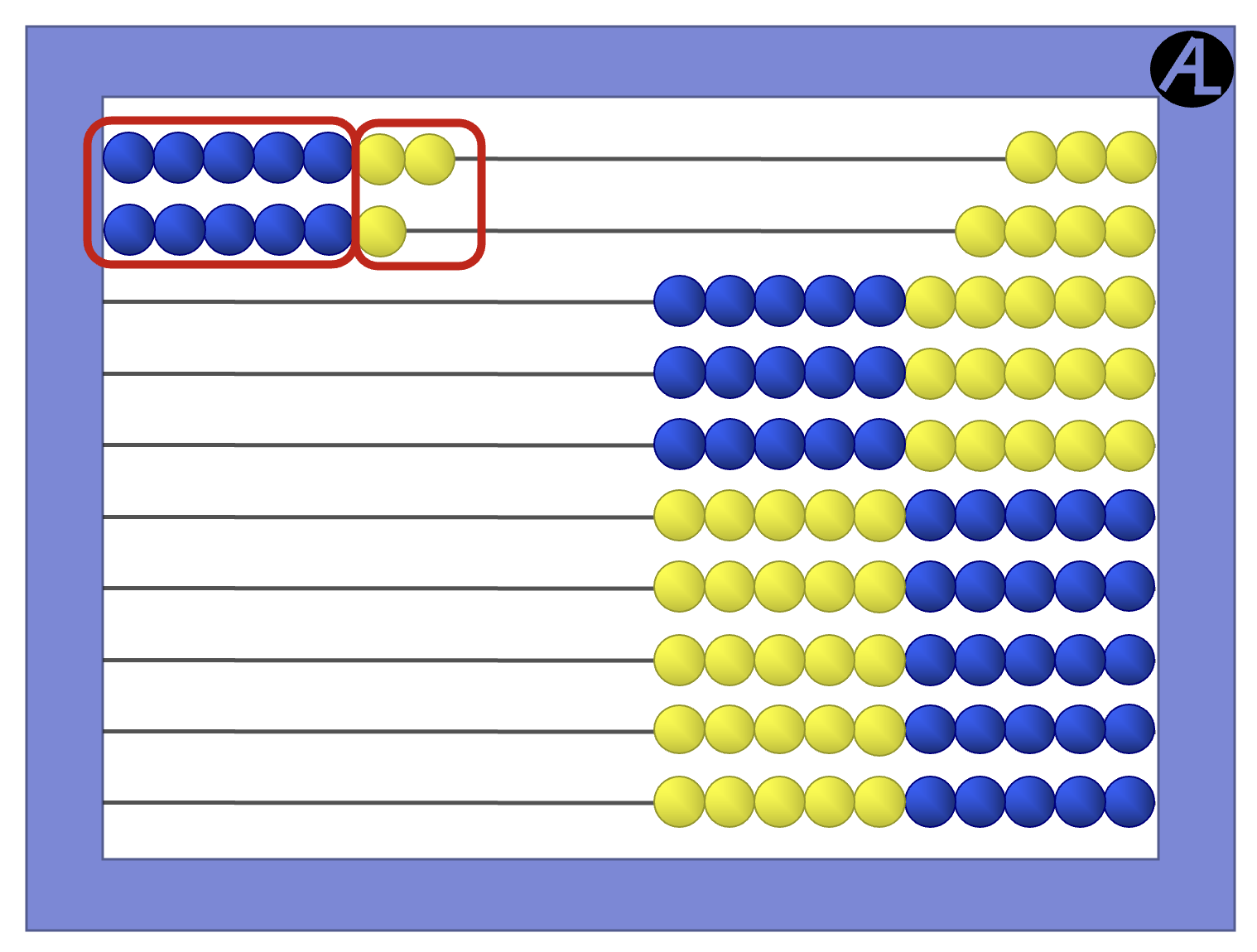
Some children may benefit from using their hands with this strategy. Think 7 is 5 and 2; show two fingers on the left hand; think 6 is 5 and 1; show one finger on the right hand. Combine the fingers and think 7 + 6 = 10 + 3 = 13.

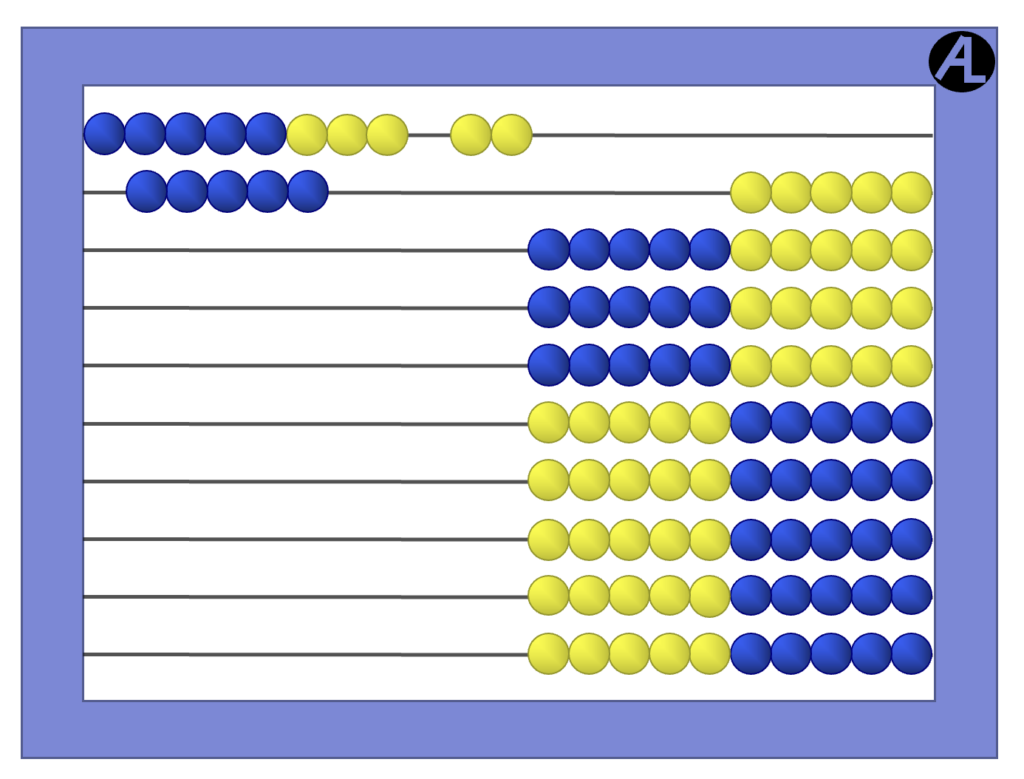
One final addition strategy is the Complete the Ten Strategy. The goal is to take enough from the smaller number to make the larger number into a 10. For example, for 8 + 8, take 2 from an 8 and give it to the other 8, making 10 + 6 = 16.

Note that a doubles strategy is not included. One textbook author claims that children learn the doubles easier, but it’s not known why. The truth is children do not find the doubles any easier, but parents and teachers drill them more.

Keep in mind that a child is considered to know a fact if the answer is given in 2 to 3 seconds.

This fact retrieval does not need be instantaneous. This two to three seconds thinking time is enough for the child to think through a strategy when necessary.

On the other hand, flash cards discourage thinking. A different part of the brain is involved in rote memory, as compared to mathematical thinking. Rote memorization is built on sand needing frequent restoring, whereas strategies provide a solid foundation. Many children with learning disabilities simply cannot rote memorize. Sadly, many adults blame flash cards and timed tests for their math anxiety.

Subtraction 

In the example, 5 + ___ = 8, 5 is the known part and 8 is the whole. The equation can also be written as 8 – 5 = ___.

Subtraction can be thought of as finding a part when the whole and the other part are known.

Avoid saying 8 take away 5. That’s bad grammar: where is 8 taking 5? And that’s bad math because subtraction sometimes is considered going up as in the above example. The correct word is minus. 

Only three subtraction strategies are necessary for mastering the subtraction facts. Be sure the children understand that 15 is 10 and 5.

The first strategy is Going Up. Let’s use 15 – 8 as an example. Start with 8, go to 10 and note that 2 is needed to reach 10, and then 5 more is needed to go from 10 to 15. Combining 2 + 5 is 7, so 15 – 8 = 7.

The second strategy is Taking Part from Ten. Using the same example, 15 – 8, subtract 5 from 15, leaving 10. Subtract the remaining 3 from the 10, leaving 7 as the difference.

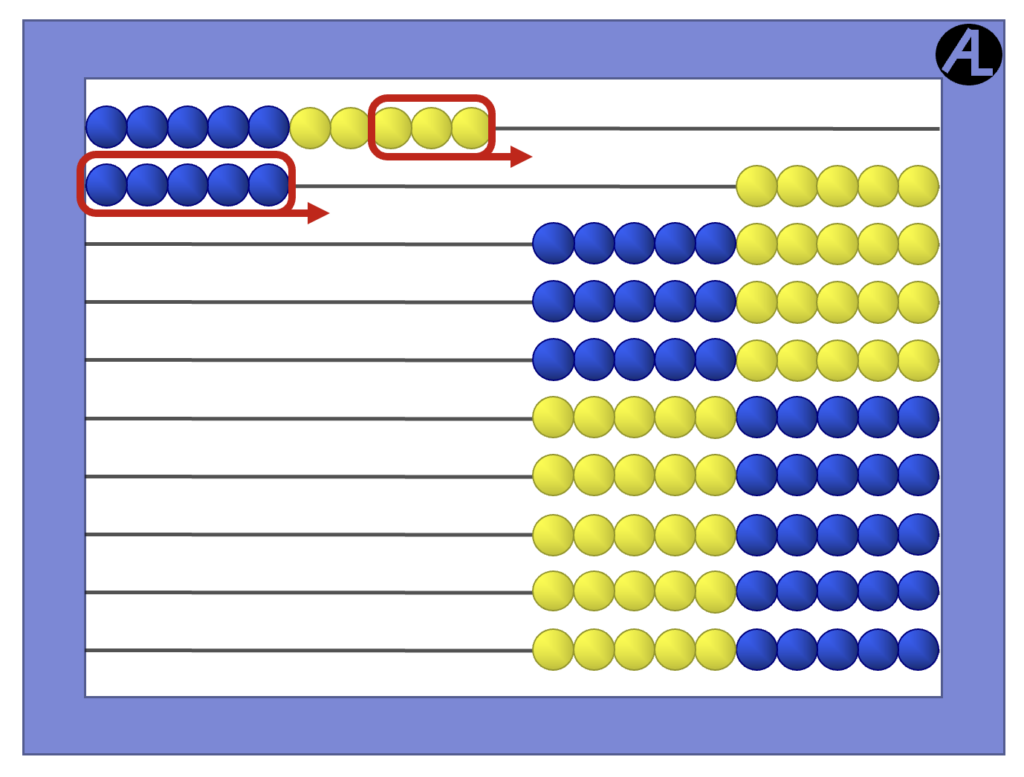
The third strategy is Taking All from Ten. Again using the same example, 15 – 8, subtract the entire 8 from 10, leaving 2, and add that to the remaining 5, again getting 7.

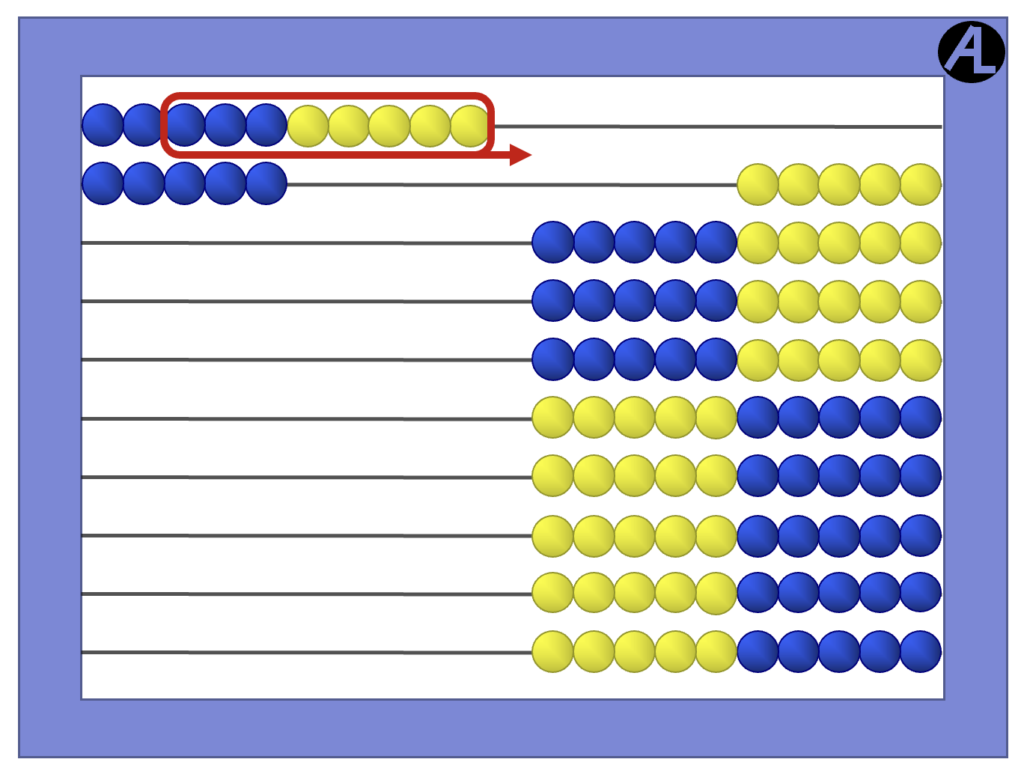
This All from Ten strategy was used extensively in the Middle Ages. Back then, they did not memorize any facts subtracting from 11 to 18; they always used the Taking All from Ten strategy!