A few years ago while on a shuttle to speak on math at a convention, I started talking to a young man next to me. When he found out I was involved in math, he said he could solve story problems as long as someone told him what operation to use. The young man didn’t realize that the essence of solving story problems isn’t performing calculations, but rather deciding what procedures to use. The purpose of learning math is solving problems; calculations are only a part of the equation.
General Considerations
Keep in mind that a problem is not a problem if the solution is obvious. If I am making my favorite recipe and have all the ingredients, I have no problem. But if I am missing an essential ingredient, I have a problem.
Unfortunately, traditional textbooks had a part in promoting a misconception regarding story problems. Worksheets consisted of a group of exercises, followed by a few story problems. Invariably, the problems were solved by the same operation as the one practiced in the exercise. So, the student didn’t bother to read the problem, but merely performed the practiced operation on the numbers in the story.
Later, when these students attempted to solve a diverse set of problems, they often try in vain to remember the lesson where they learned how to solve that particular problem. The details of those long forgotten lessons are missing.
Katie was a victim of that type of math learning. In her early twenties, she decided to go to college, but was scared of taking of math courses. She told me that there was so much to memorize. She didn’t realize math is not about memorization, but understanding. Solving problems is about thinking, not trying to recall a particular specific procedure. No one could possibly remember how to solve every type of story problem.
Some people are under the impression there is only one way to solve any problem. Actually, solving a problem in a different way is a check on correctness, an important consideration in real life. Or, another way to look at it: if humans didn’t find new ways to solve problems, we would still be living in the Stone Age.
Problem solving starts when a preschooler assembles a jigsaw puzzle. Through such work the child masters frustrations, acquires perseverance, learns there is more then one way to do the puzzle, and experiences the joy of success. The role of the parent or teacher is to provide the appropriate puzzle, prevent distractions, offer bits of encouragement, and rejoice at its completion.
For simple addition and subtraction problems, use part/part/whole circles. A larger circle, the whole, is drawn above two smaller circles, the parts, with lines connecting each part to the whole.
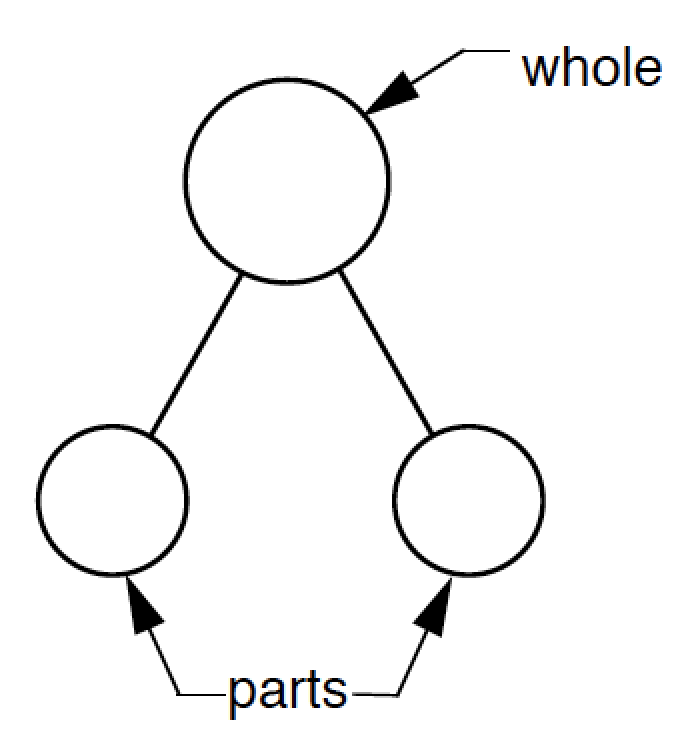
Let’s use the part/part/whole circles to solve this missing addend problem: “Lee received 3 goldfish as a gift. Now Lee has 5. How many did Lee have to start with?” Is the 3 a part or a whole? A part. Is the 5 a part or a whole? A whole. What is the missing part? 2. It doesn’t matter if this problem is considered addition or subtraction, young children can solve the problem.
Another tip to help younger children solve problems is to change the problem by using their name and their circumstances. In other words, personalize the problem. It’s also helpful for children to make up their own problems. Of course, everyday events frequently lend themselves to great story problems.
One thing to avoid is teaching the child to look for key words. That is, do NOT teach that “altogether” or “sum” means add or “times” and “of” means multiply. Do you look for key words when solving real-life problems? I like to write problems with the wrong key words.
Children should not expect to know how to solve every problem. Problems are sometimes used to teach a math concept. A Japanese teacher will give the class a problem to work on in pairs. Then she asks the students to explain their solution to the class. The solutions are presented with the simplest first and the most sophisticated last. Everyone learns some math this way. Mistakes are treated as a normal part of learning.
Sometimes textbooks use the format of a story problem to ask a rote question. One such example is: “Percy has 342 pencils. How many tens does he have?” This is nonsense. The textbook wanted 4 as an answer, but actually Percy has 34.2 groups of ten pencils. The student is not learning to make sense of mathematics, but to satisfy the textbook.
Sadly, achievement tests often put a simple question into a story format. For example, to check whether the student can read an analog clock, the test might ask, “Sophia’s violin lesson starts at the time shown on the clock. What time is that?” This is unfair to the child who is struggling to learn to read or to master English as a second language. Asking for the time on a simple clock will do.
Some Tips
Generally, math problems need to be read several times. I told a group of home schooled middle-schoolers that even mathematicians read problems more than once. They were astonished.
Often a simple sketch can make a problem seem clearer. Some textbooks do this unnecessarily for the students. The student learns more by making their own sketch.
When a child gets really stuck, tell them to leave the problem and go do something else. Their brain will continue working in the background. When they return, they will probably have new insights.
Who has ever completed a puzzle by always finding the wanted piece on the first try? What baby has learned to walk without frustrations and falls? Studying math, or anything else for that matter, will be frustrating at times. Persistence is required for success.
Thanks so much! My daughter is on book A but I really appreciate these insights not to mention the curriculum itself! I recently learned of a new math program designed for older kids to help them to
conceptualize math. My daughter, through RightStart, is learning it from the very beginning. We both love it!