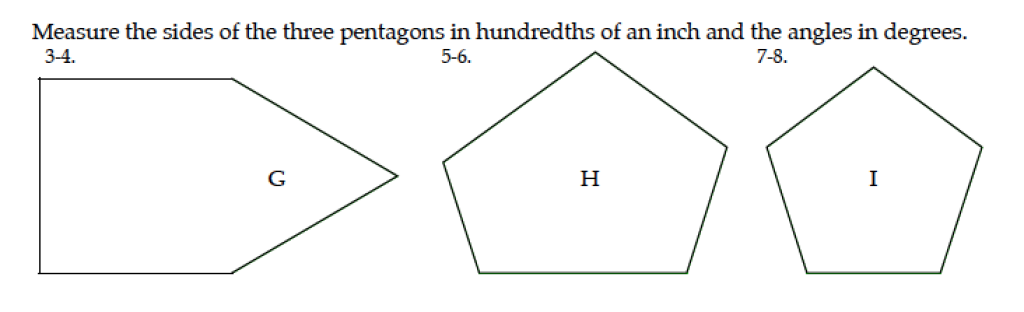
This week’s discussion on taken from RS1 Level E, Lesson 104. Well, actually, it’s more related to Worksheet 115, the worksheet for this lesson. The lesson is on classifying polygons, but the problem spot is the measurements of the pentagons, questions 3 through 8.
I spoke with Sheri and her son Diego this week and Susan and her daughter Jamie last week about this questions. I know there more of you out there with this question, so let’s get this addressed and explained.
The instructions on Worksheet 115 says to measure the sides of the three pentagons in hundredths of an inch and the angles in degrees.
The angles are pretty easy – use the goniometer and measure away. The challenge is the measurements to the hundredths. The 4-in-1 ruler has measurements to the sixteenths. And to the tenths. But not the hundredths! Now what?
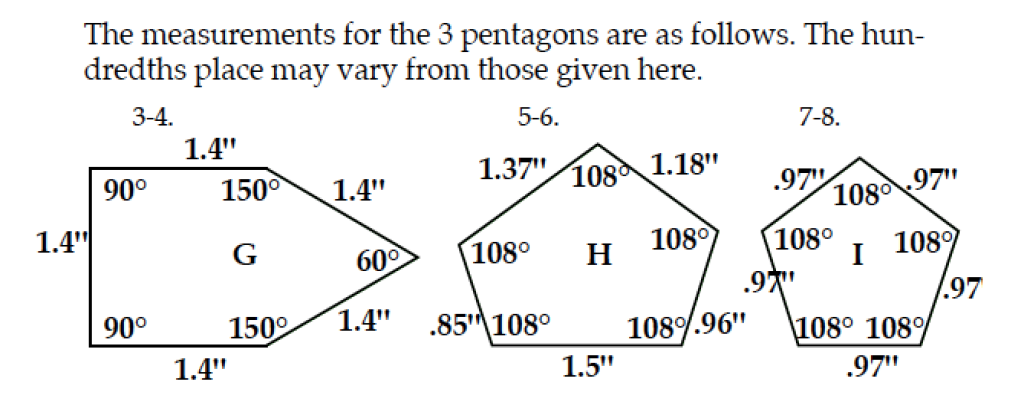
We are asking the child to do a bit of estimating here. Using the ruler with inches broken into tenths, we can see that this line is more than 1.3” and less than 1.4”. Looking at the way I have my ruler lined up here, I’d call that 1.37” or 1.38”.
Lesson 104 gives the answer as 1.37”. Notice that it also says “The hundredths place many vary….” So if the child says 1.36” or 1.37” or 1.38” or 1.39”, that’d work. We know it’s not quite 1.4” and it’s definitely not 1.3”.
So why are we having this child do this? Why estimating? Don’t we want them to learn to be precise?
One of the children was thinking the measurement was 1.4”. Here’s the application of precision. If we don’t quite start the measurement of the line right at the zero mark on the ruler, then the measurement looks more like 1.39” or 1.4” as shown incorrectly here. Notice how my measured line isn’t quite starting at the zero mark of the ruler?
Also, when using the 4-in-1 ruler, it helps to lift the ruler a little to “roll” as shown. This allows the ruler to be closer to the line being measured, makes the reading of the measurement easier, thereby increasing the accuracy of the measurement.
What is the point of this exercise? The concept here is that it is difficult to measure precisely because you can always be more precise. If I had a ruler that measured to the hundredths, we’d know if this line was 1.37” or 1.38”, but could still say that it could be measured more precisely to the thousandths, maybe 1.375″.
This is a skill that is used often and is necessary in everyday life. It depends on what we’re measuring and what units we’re measuring in.
If we are measuring the distance from home to the grocery store, miles is acceptable. Or maybe blocks, if you’re close. If we’re measuring the length of the house, miles is silly, but measuring in feet is good. Inches would be overkill. If we’re measuring the edge of your computer screen, inches is good; feet is too much and inches to the tenth is generally not necessary.
At this point, we’re not expecting the child to know all this. We’re simply exposing the child to the idea that you can measure more precisely that it first appears.
One final note: in the RightStart™ Mathematics first edition, notes and comments like this are not available in the lesson. In the second edition, we try to give you as many explanations as possible. These explanations tell you why you’re doing what you’re doing, what the research is behind something, or what to do if a child is having difficulties or is advanced. When this topic is addressed in RS2 Level E (due summer 2016), we’ll be certain to include an explanation!