Today’s blog is thanks to Joanna and her son, Hunter. They live in Florida and started with Level A and are now working on Level H!
Here’s Hunter working on Level H, Lesson 82…..
This lesson is on pyramids. One of the goals of the lesson is to find the surface area and volume of a pyramid. And that’s where we all stalled out, myself included, once we tried to apply the lesson to the worksheet.
This is what we have on the worksheet:
Constructing the pyramid with the Geometry Panels and drawing the net: no problem.
Then, for Problem 2, we are to find the volume and surface area of the pyramid. Now we have a challenge!
Let’s start with the surface area. For me, that’s easier. Because I’m the writer here and letting you share in my confusion and subsequent learning, we’re going address this the way my brain thinks!
So, surface area. We need to add up the area of the square base and the area of the four triangle sides: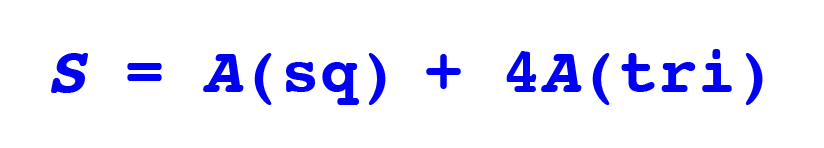
The worksheet tells us to use decimeters to two places. Using my handy-dandy ruler, I know the side of a panel is 10 cm or 1 decimeter (dm). So what’s the area of the base of this pyramid? It’s the width times the height, or w × h. That’ll be 1 dm × 1 dm. Area is 1². That was easy.
Now we need to figure out the area of the triangles. What’s that formula? Area of a triangle is half of the width times the height:
We know the width, or base, of the triangle. It’s 1 dm. But we don’t know the height! Let’s look at the picture again.
Take a closer look. What are we looking for? We are looking for the area of one of the side panel triangles. Let me draw it out…..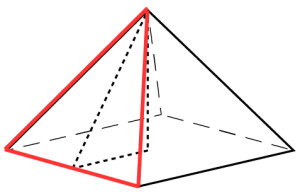
Looking at the formula, we know the base. It’s the same measurement as the side of the square; 1 dm. Actually, because this is an equilateral triangle, all the sides are 1dm. But the height? We could measure, but that’s not very accurate. I know! Let’s use the Pythagorean Theorem:
Divide the triangle in half. This will be our height measurement.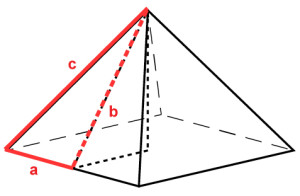
Now, using the Pythagorean Theorem, we know the measurement of the base, a; it will be half of 1 dm, or 0.5 dm. The measurement of the hypotenuse, c, is 1 dm. Plugging our numbers into the formula and exchanging b for height, or h, we have the following: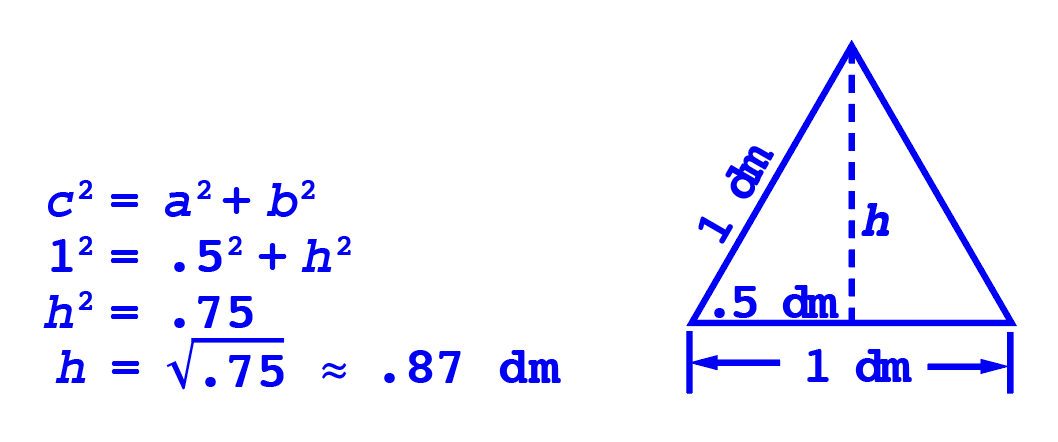
Alrighty! We’re on a roll now!
Now we have the height of our triangle. Next is the area of the triangle.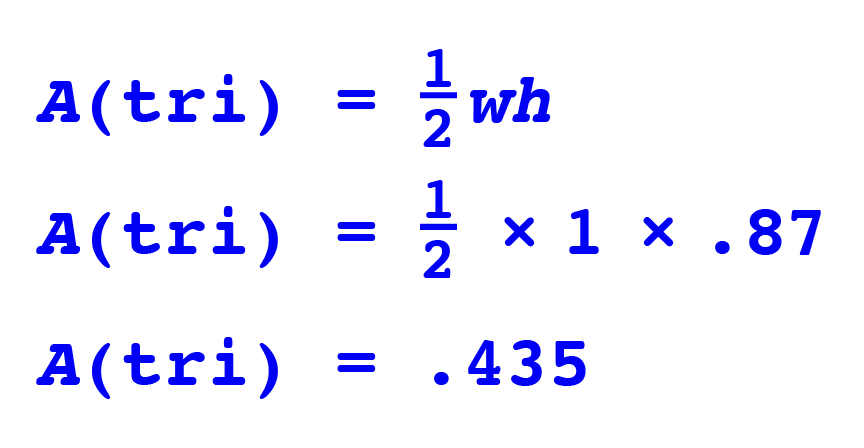
Good. And finally the surface area of the pyramid…..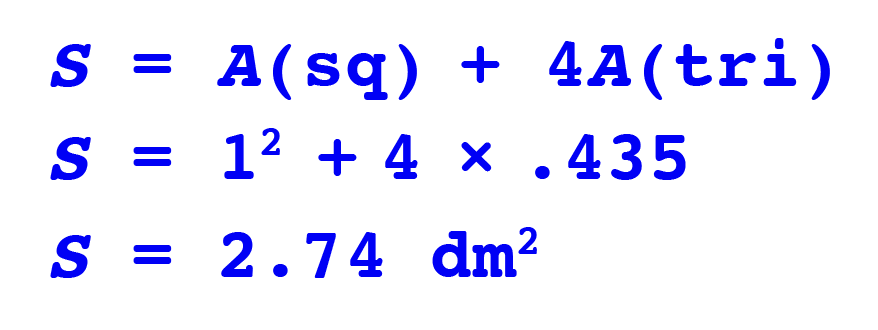
Well, once we figured out how to get the height of the triangles, that wasn’t too bad, right? That was the part that hung me up. The rest was pretty easy.
Now let’s tackle the volume of the pyramid. How do THAT? Well, look back to the lesson. It’s right there!
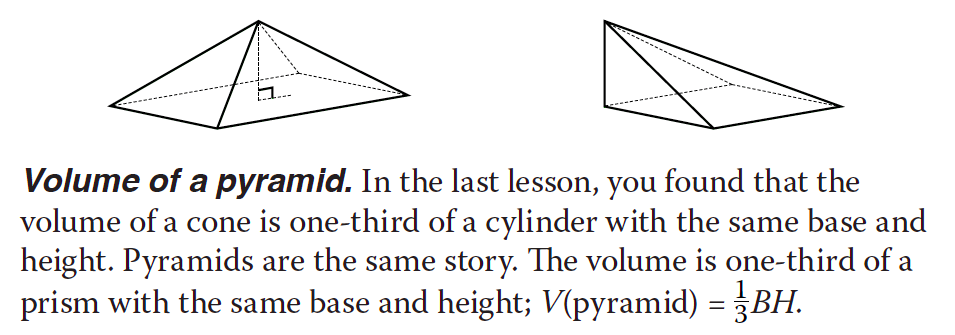
So we have this to work with:
We’re using a capital B and H for base and height because these are different measurements than we used for the surface area of the pyramid. Here’s the translation:
Base area is 1 dm × 1 dm, or 1². We already figured that out, remember? Now for that pesky height measurement again.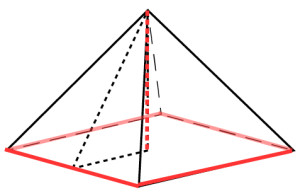
Got any clues? How about this…..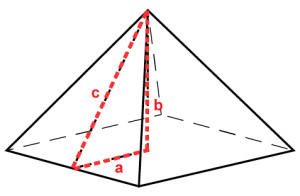
Using the Pythagorean Theorem, we know the base, a; that is half of 1 dm, or .5 dm. The measurement of the hypotenuse, c, is known from our previous calculation of .87 dm. Plugging our numbers into the formula, we come up with the height of the pyramid, or H, as .71 dm.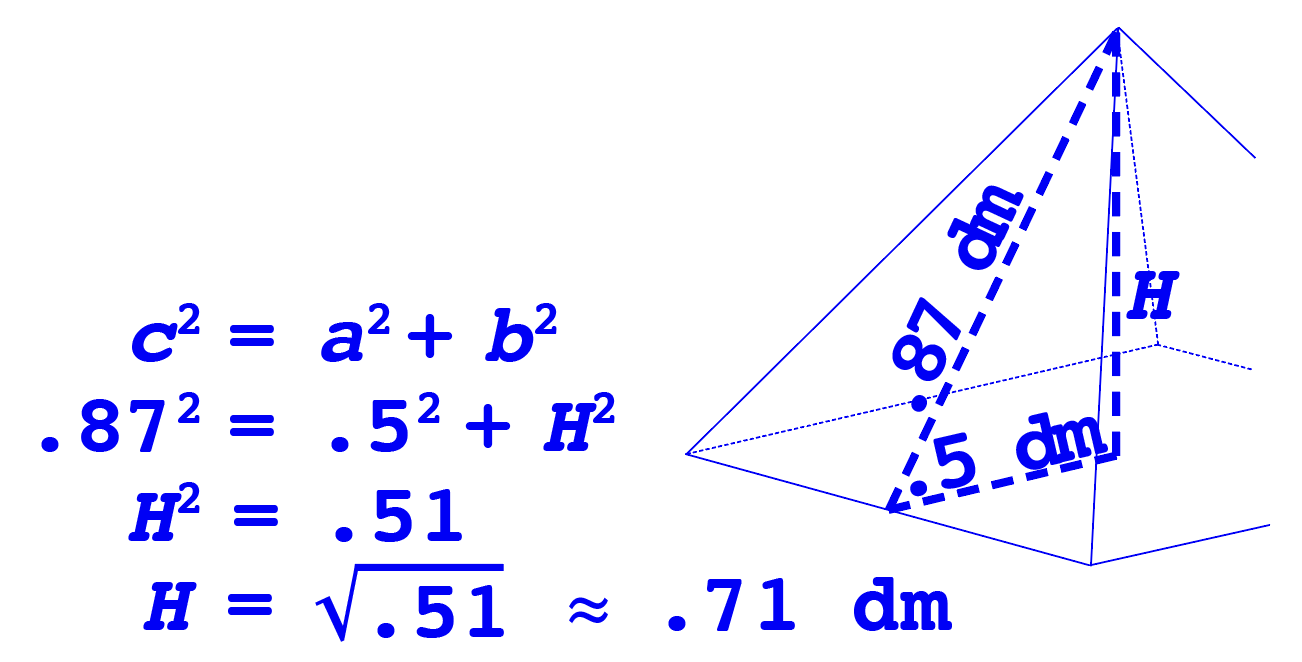 
How that we have the height, we’re back in business.
And the volume for this pyramid is…..
So, one more thought for you all. Why, oh why, didn’t the worksheet just give us these measurements? Or at least a clue?? Well, that’s the way real life problems occur. Sometimes we only have one piece of the puzzle, but if we look at other things we know, in this case the Pythagorean Theorem, we can figure out the missing pieces of information with a bit of maneuvering. And we did just that!
