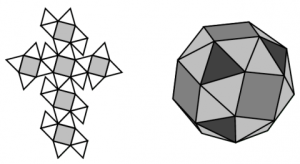
A customer called yesterday with an interesting question. She and her son were working on Lesson 103 in RightStart Math Level H, second edition. They were making a snub cube using the RightStart™ Geometry Panels and couldn’t get the net to work out. She was wondering if there was an error.
For those of you that want to know the short answer and not the details: the lesson has it right. The net does, in fact, become the polyhedra shown above.
For those of you that want to know the long answer and hear the story, settle in, and let me tell you the fun we had!
First of all, what IS a snub cube? A snub cube is one of the 13 Archimedean solids. It is formed by adding extra triangles around the squares of a cube. Specifically, 32 triangles are added around each side and vertex (point where the lines meet) of the squares.
I had two of our summer helpers work on this problem. Katie was a very bright college student and Logan was a high school senior and valedictorian of his class. They put together the net (pictured above on the left) with ease. However, they struggled to get the floppy pieces to shape up into the snub cube.
I checked on their progress after a while. I only added to the confusion. It just wasn’t working, which is what our customer had experienced.
I told Katie and Logan to approach this from a different perspective. I said, “Let’s build this by looking at the shape and recreating it.” Given that we hadn’t made any success with first method, both were eager to try a new tactic.
We started with the square on the right side of the shape pictured above. I said, “See how each side of the square has a triangle attached? And each square corner has two triangle points coming into it?” OK, I should have said “vertex”, but I didn’t.
I continued, “Then, when you have the square and 12 triangles attached, rotate, attach a square in the right spot, then build the same 12 triangles around that new square….” Katie and Logan jumped in and began building.
There was a small problem in the construction because Katie and Logan didn’t realize that two triangle vertices meet at the square vertices. Yes, I had told them that, but they didn’t apply what they had heard. We’ll address that issue in a minute…. After a quick conference and discovery, they went away and, in practically no time whatsoever, came back with a perfect snub cube and smiles all around!
I then challenged them to make the left handed version of the snub cube building the net then assembling, just to see if they could do it. They went off and came back shortly with a newly constructed snub cube.
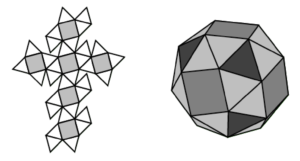
I asked why they had no problems with the second net when the first was nothing more than a tangled mess. Katie responded, “Once we knew the pattern of two triangle points touching the corner of the square, it was easy!” Logan added, “The first time we did it, we were randomly attaching triangles here and there, which didn’t work! ”
So what have we learned here? First, when someone tells you something, it isn’t as effective as discovering and doing it yourself. I told Katie and Logan that each square corner has two triangle points coming into it. They heard me, but didn’t understand until they discovered it themselves, applied it, then developed the understanding for future situations.
Dr. Joan A. Cotter says, “What one discovers and understands is remembered better than anything learned by rote.” This knowledge made the second snub cube a breeze.
A second thing learned is patterns! Logan said, “It was easy going when we knew the pattern.” Once a pattern becomes evident, the randomness of a situation becomes organized and manageable. This can be applied to other polyhedras, to math in general, and to life as a whole.
P.S. Look at the polyhedras shown above. See any special patterns with the dark triangles? They share vertices with three squares and share edges with only other triangles. The lighter triangles share an edge with a square. Hmmmmm…..