As you probably know, we are starting our free webinar series. We had a blast this week talking with everyone and are looking forward to next week. Watch for the announcement on Sunday…..
After the How to Teach RightStart™ Mathematics Level E webinar, I got to chatting with Kate. She and her son are in Level E and she wondered how to help her son with the puzzle numbers. He was uninterested in the challenge and was rapidly losing interest in math altogether. I thought this would be a fantastic topic for this week’s conversation.
First of all, what are puzzle numbers? They are introduced in Level E, Lesson 6, and initially referred to as equation puzzles. They are used pretty consistently throughout the first half of the year. The best way to explain what they are is to show you.
Using these four numbers shown below, write an equation using math symbols such as =, +, –, ×, ÷, ( ), and /. The numbers must stay in the same order. Can you see any options?
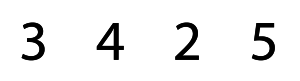
First one I saw was 3 + 4 = 2 + 5. Did you see that one too? How about 3 + 4 – 2 = 5? That works too!
Let’s try another puzzle. How about these numbers:
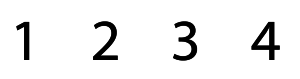Any thoughts? Think it over before you check out my answers…..
The first one I found was 12 = 3 × 4. I will confess to peeking at the lesson book for 1 – 2 = 3 – 4 and -1 + 2 = -3 + 4. Yes, we can use negative numbers too!
Kate’s son wasn’t too thrilled with these puzzles. He was struggling and didn’t enjoy the challenging. I proceeded to tell Kate the source of the puzzle numbers and that ramped up the fun. So now I’m going to tell you where this idea of puzzle numbers came from!
When Dr. Cotter was a little girl in Madison WI, the license plates on vehicles were four digits. As the family would travel about, young Joan would look at the passing cars and see if she could make an equation out of the license plate. Here’s an old license plate:
Do you see any possible equations in this license plate? How about 2 + 9 = 8 + 3? Do you see another? I see at least two more. I’m going to let you puzzle through this yourself. Post your findings in the blog comments below!
I was working with a school in Florida a number of years back. They were working on the puzzle numbers for the lesson warm-up. The day’s numbers were as follows:
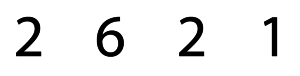
What are you seeing for equations? How about these: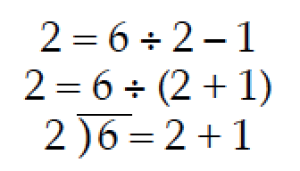
One young man was unconventional and read the numbers from right to left, rather than left to right. He did keep them in order! He came up with 12 = 6 × 2. What a phenomenal thinker! He looked beyond the assumed rules, kept the numbers in order, albeit from right to left, and made an equation! Now that’s an individual that will make a difference in the world.
So how do we help a child face the challenge of the puzzle? Sometimes knowing the source and reason surrounding the situation is helpful. Sometimes a child has breezed through their earlier math experience and hasn’t learned how play with and persevere through a more challenging situation. Sometimes a child simply doesn’t know the fun in math!
If a child is not experiencing fun in math, I wonder if they are playing the card games enough. The games are the review and practice in a fun and enjoyable setting. The emotions we experience while we learn something are frequently attached to the new information. Ironically, Kate and her son had not been playing the games. Kate said that is going to change immediately!
I challenge you to find and enhance the fun and joy in math this week. Have a great day and go play a math card game!
2 / 6 = 2 + 1 ?? That’s a puzzle to me.
2 + square root of 9 = 8-3 Couldn’t find a square root sign
2 + (9-8) = 3
Oh my! Error!! I corrected it…..
Our son is doing these this year as well. Some of the answers in the book are fairly abstract. As a test, I started to do the puzzles alongside my son and do get a couple of the book’s answers (I got a Master’s degree in a math intensive field) but usually not all of them.
Our strategy has been two fold, after letting our son try the puzzle for a couple of min. First, I write out the answers, sometimes making a purposeful mistake and let him determine if the answer is correct or not … very helpful to make sure that he understands the proper order of operations. Secondly, I may write out part of the answer, mostly for the abstract portion of the answer, and let him finish the equation.
Scott
Most of my kids love the equation puzzles, but one didn’t. She is currently in E. She couldn’t see any equation in the numbers. The four digits were overwhelming. I encouraged her to keep on trying by putting “=” in different places to see what she could discover. For example, in 2 9 8 3, she might first put “=” like this: 2 = 9 8 3; then what operations are needed to make the equation work? In this case, I’d put -2 = 9 – 8 -3. Here I could manipulate the signs to make another equation. Then I’d move on to put the “=” after 9, and so on until “=” has visited all legal places. She is getting pretty good at this and enjoying it.
Both of my sons have HATED the number puzzles and also a friend’s daughter. My friend showed her husband what the struggle was. He tried to figure it out and had a really difficult time…he is a surgeon. So since I was have the same trouble, I gave a number puzzle to my husband. He had a difficult time figuring them out also…He took a few to work to see if his co-workers could get them more easily than he did…nope…they all struggled too. They are all Mechanical Engineers. After this point, I changes how I presented them. I would give the numbers and the equation signs, but not in the appropriate order…then have them try to place them. At least this way, they felt they had a chance!
Great idea!!
-2=9-8-3
I had two students in E last year. At first they struggled with the number puzzles. I gave them some tiles (similar to Scabble tiles) with numbers and operation symbols on them. They could then manipulate the operation tiles between the number tiles to try various ideas for equations. I had to show them how to do the first few so they would get the hang of it. After a while, it became a race to see who could come up with an equation first – or even more exciting for them was to try to come up with a correct solution that was not in the book! Even after they were quite adept at this exercise, the puzzle solutions that included exponents and square roots were almost beyond them. However, although neither student had had any exposure to negative numbers, and although I did not teach it to them, they both figured out negatives on their own (with a solid understanding) with these exercises! I’m still not sure how it happened. 😀