Dr. Cotter and Geometry

For years geometry was not considered a topic that primary students could or should study, even though they are surrounded by geometrical shapes. Some second graders I worked with didn’t consider their geometry work to be math, until they saw numbers included in their work.

Sometimes teacher education programs provide little guidance on how to teach geometry. I know an elementary teacher who graduated recently with no geometry in either high school or college!

Geometry and Math

Geometry is more than quantity; geometry is about measurement and relationships between those measurements.

• To determine length, we need a linear unit.
• To determine area, or surface space, we need to find the number of squares having sides 1 unit long that fill the area.
• Then, to determine volume, or space, we need to find the number of 1-unit cubes that fill the space.

Because the lengths being measured aren’t always whole numbers, fractions and decimals are needed.

Some relationships introduced other new numerical values. There is no unit that will produce whole numbers—not even fractions or decimals­—for both a side and a diagonal of a square.

The diagonal in a square equals the length of a side times the square root of 2, which is approximately 1.4142135. 

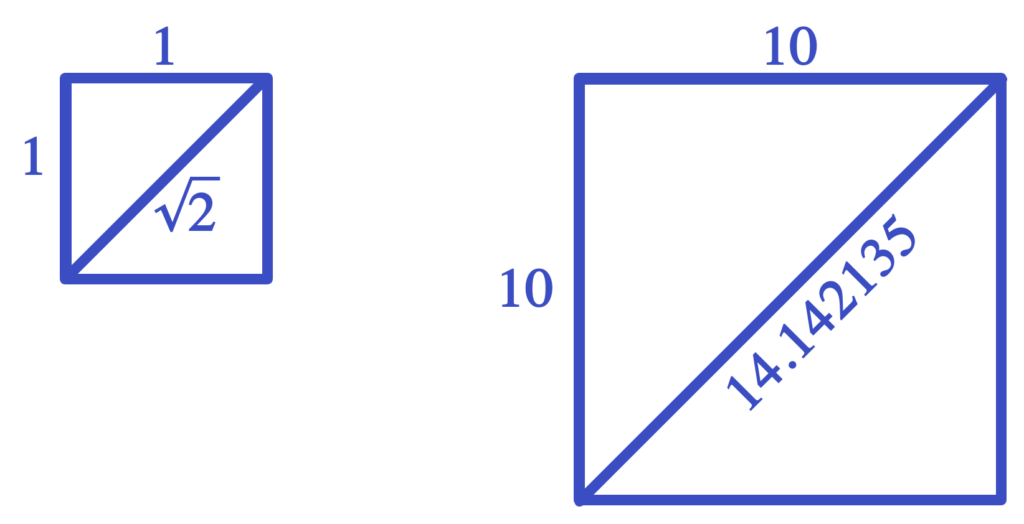
If the sides are 1 unit long, the diagonal is the square root of 2. If the sides are 10 times longer, the diagonal is 10 times longer than the square root of 2, which is approximately 14.142135.

Another example of these relationships lies in a circle. The diameter fits around the circumference a little over 3 times. Since this ratio is not an exact fraction or decimal, it is given a special name, pi.

Teaching Geometrical Names

Today, most standards for the earliest grades recommend teaching the names of common geometrical figures and objects. This is not as simple as it sounds.

For example, consider a rectangle.

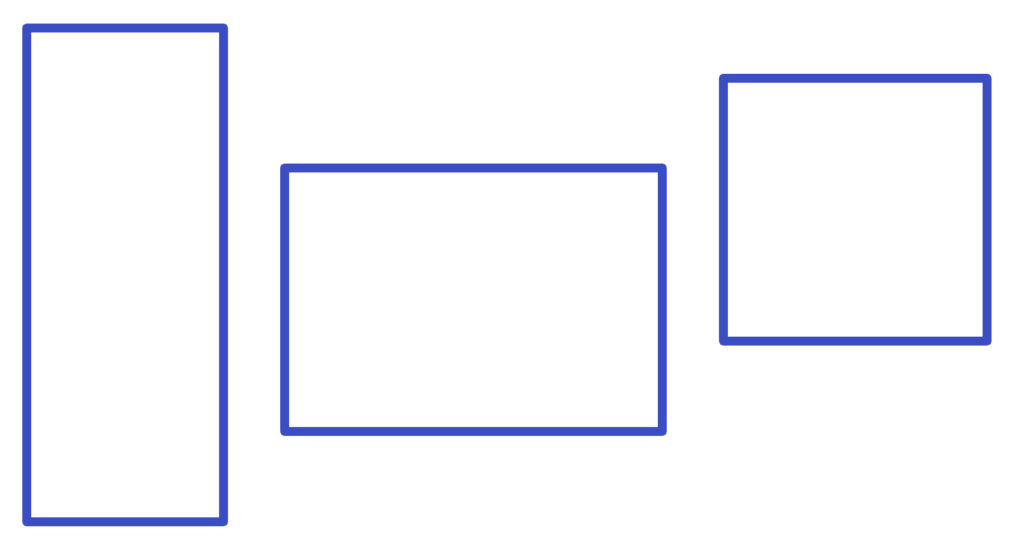
First of all, what is the definition of a rectangle? It is a quadrilateral (four sides) in which all four angles are right angles (90º) and opposite sides are parallel.

Does the longer side of a rectangle need to be at the base, or bottom? No. Curriculum for a well-known preschool program refers to a rectangle as “long and low.” Sadly, that’s one definition that will have to be unlearned.

Can the four sides of a rectangle be congruent? In other words, can the four sides be equal? Yes.

And yes, a rectangle can be a square—albeit a special rectangle. Did you notice the definition of a rectangle says nothing about the length of the sides? It only says is that the opposite sides must be parallel.

Triangles frequently suffer the same fate as rectangles. Children are often presented with an equilateral triangle as a model. Andy, 5, was adamant that a triangle must have all the sides equal.

Triangles are often shown as having one edge parallel to the bottom of the page or table. Children need to see all types of triangles in all types of orientation.

Five-year-olds enjoy learning about equilateral, isosceles, and scalene triangles, as well as acute, right, and obtuse triangles.

A more difficult problem for some children is distinguishing between two- and three-dimensional figures. I showed Jonathan, 4, a paper plate and reminded him it was a circle. Then I showed him a ball and told him it was called a sphere. He knew they were both round, but he really had to think about the sphere. 

Until I was about 9 years old, because of an eye problem, I lived in a two-dimensional world. I remember asking people how can bricks turn a corner. I didn’t understand that bricks had depth as well as width and height.

To understand cylinders, prism, and pyramids, children need to touch and explore these objects just like Jonathan did with the sphere.

Babies are born into a 3D world. Yet electronic screens and television screens, along with workbooks, flatten children’s perceptions into a 2D experience, especially once they start school.

Drawing Board Geometry

Children learn by manipulating and creating new objects. Since the time of Euclid, to make geometric constructions, traditional geometers, persons skilled in geometry, use only a straightedge and compass. No measuring was permitted. Complying with these restrictions made it very difficult for children to delve into the wonders of geometry.

As a freshman taking an engineering drafting course, I was introduced to the drawing board and tools: T-square, triangles, and compass. When my daughters were around 7 and 8, I located the equipment, substituted a simpler compass, and showed them how to make some constructions. To add some color to their work, they did the following: they traced over their work with colored markers and erased all the pencil lines. Even the lines under the colored portions disappeared.

A drawback to the traditional drafting tools was that the size of the equipment was simply too big for children. The board and T-square were 2 feet wide (although is nice for a student with some dexterity issues). When daughter Connie took a drafting course in college, she was provided with a smaller portable drawing board and tools for doing homework on standard-size paper. When I saw this equipment, I asked her if I might borrow it and try it with my Montessori kindergartners.

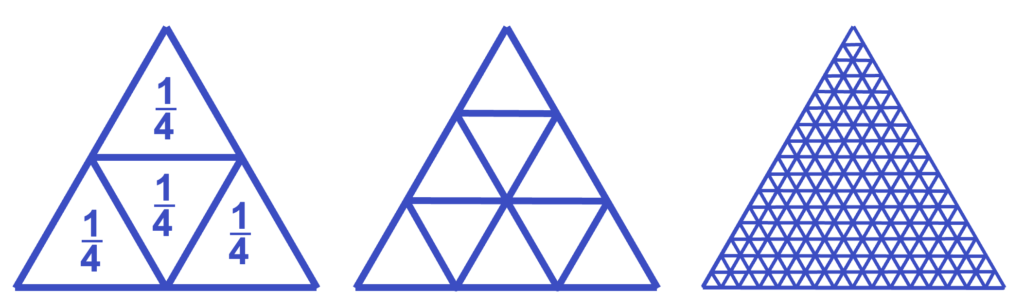
First, I showed the 5- and 6-year-olds how to construct equilateral triangles. Next they divided them into halves several different ways and wrote the fraction on each half. The children continued by dividing equilateral triangles into thirds, fourths, sixths, eighths, ninths, and twelfths. Some children also did 18ths and 36ths. One girl, Stephanie, actually divided that triangle into 256 equal parts!

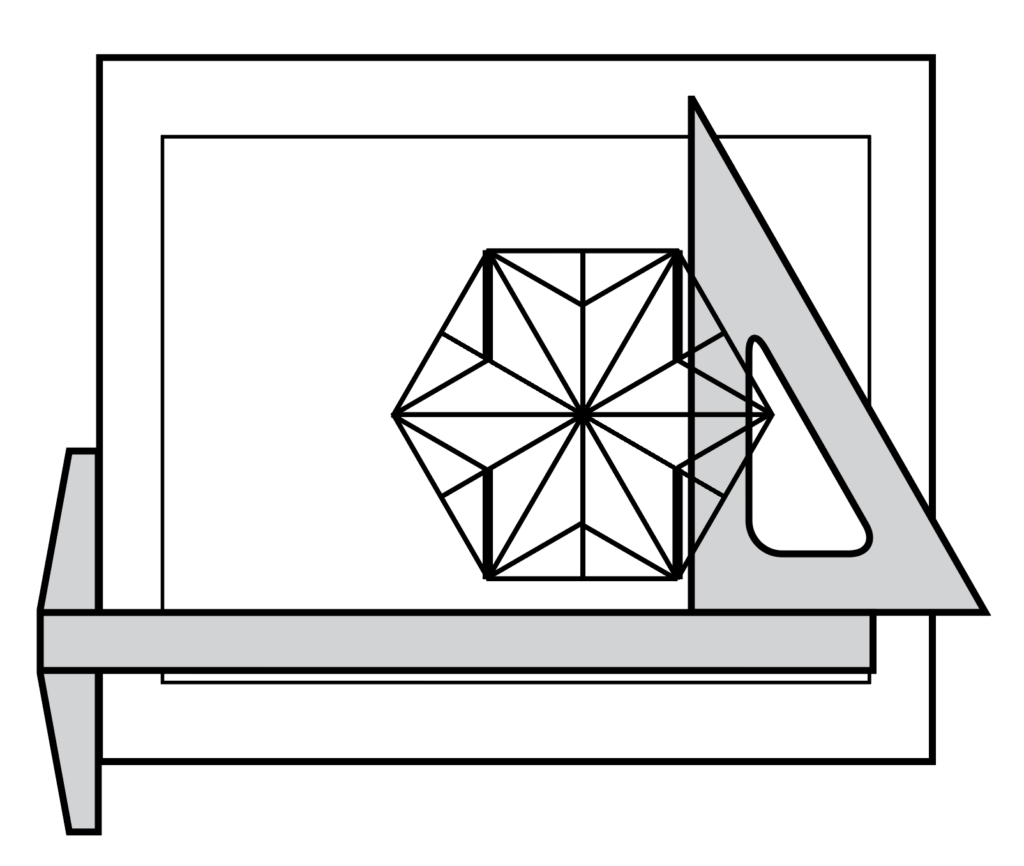
The children also constructed hexagons, stars, squares, and inscribed squares. I have demonstrated these activities to hundreds of teachers at conferences all across the United States.

RightStart Math and Geometry Lessons

These geometry activities are incorporated into RightStart Level C and Second Grade. Lines are not drawn willy-nilly. The student needs to be able to explain how they know where to draw every line. This practice of justifying every step is consistent with the whole field of mathematics. 

After a number of years, teachers asked if I could write more advanced lessons. About the same time, I realized that much of the math taught at the middle school level could be approached either algebraically with lots of equations or geometrically with visual representations. Since most preteens prefer visual information, I spent four years writing the RightStart middle school curriculum. These lessons are written to the student. The intent is to encourage them to learn how to read a math textbook and work through the mathematics more independently.

We must give children the opportunity to explore the world of geometry. This introduces them to another branch of mathematics. A child who may not excel in arithmetic may well flourish in geometry, fostering and strengthening their love for math.