Flash cards are not a good way to drill the facts. Many adults, because they could not respond fast enough to flash cards or time tests as a child, became convinced that they have no math “ability.” These people are the ones with math anxiety – sometimes even life-altering math anxiety.
The only people who like flash cards are those who do not need them.
In other words, those who like flash cards are good with their facts, don’t need the practice, and enjoy the satisfaction of their rote memorization abilities.
A problem with flash cards is that they give the false impression that mathematics is a subject that doesn’t require thinking. Or that math is just a tidy collection of “facts” that everyone must just memorize.
Flash cards are abstract; they require associating two symbols with another symbol. The theory behind flash cards, going back to 1910, is based on the faulty concept that a person learns these facts by associating these three symbols.
For example, if you see 8 and 7, you think 1 and 5, which is 15. Then, a few years later, the unfortunate child is expected to memorize 8, 7, 1 for subtraction and 8, 7, 5, 6 for multiplication. Most children find this very difficult. Brain research has confirmed that our brains do not work well this way, regardless of age.
On the other hand, a child familiar with the Cotter Abacus thinks about the concrete quantities when asked for a fact and uses strategies to find the results.
Here is 8 + 7 entered on the abacus.
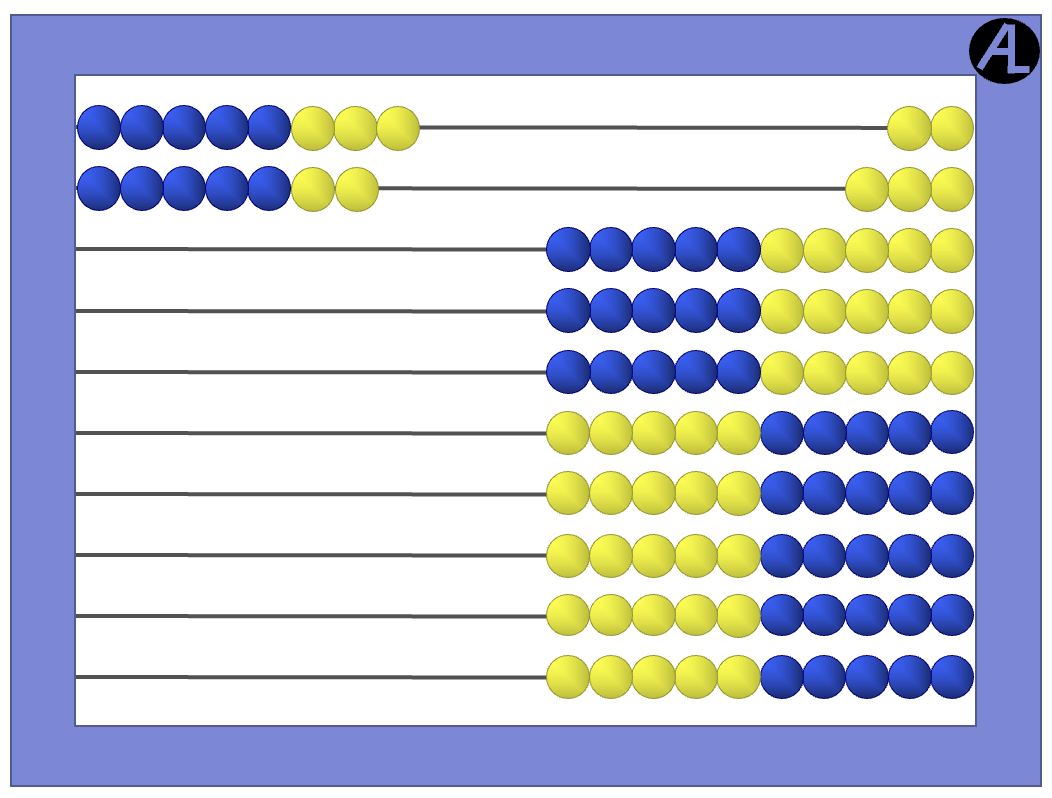
Given the grouping of the abacus beads by 5s and 10s, it is easy to see 8 as 5 & 3 and to see 7 as 5 & 2.
Group the dark beads, the two 5s, which is 10. Then see the light beads, which is 5 more. This shows 8 + 7 as 10 + 5, which is 15.
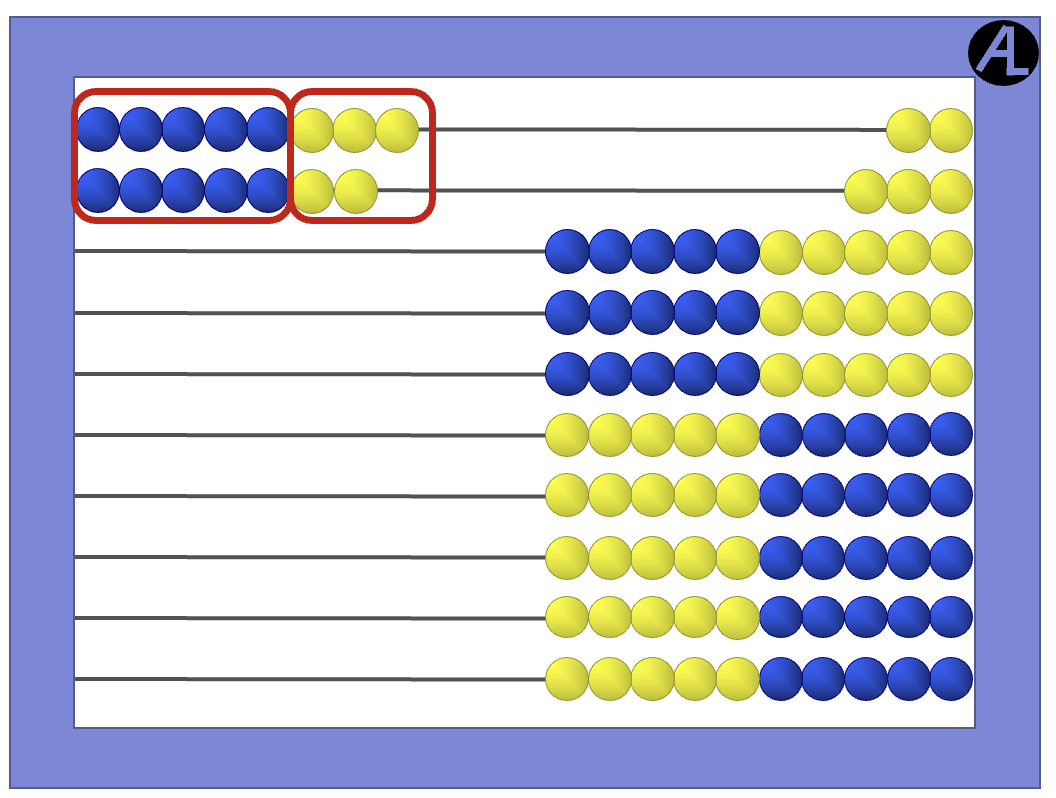
Another possible strategy for 8 + 7 is to make the 8 into a 10 by taking 2 from the 7.
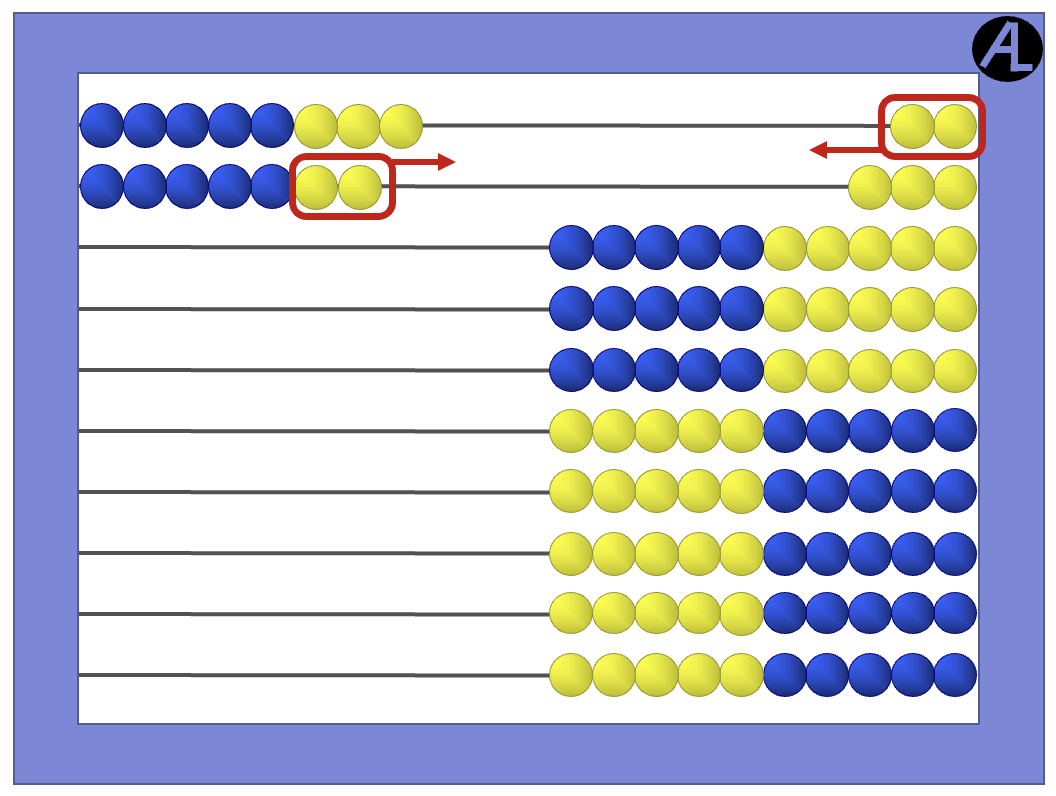
This changes the beads into 10 and 5, which is 15.
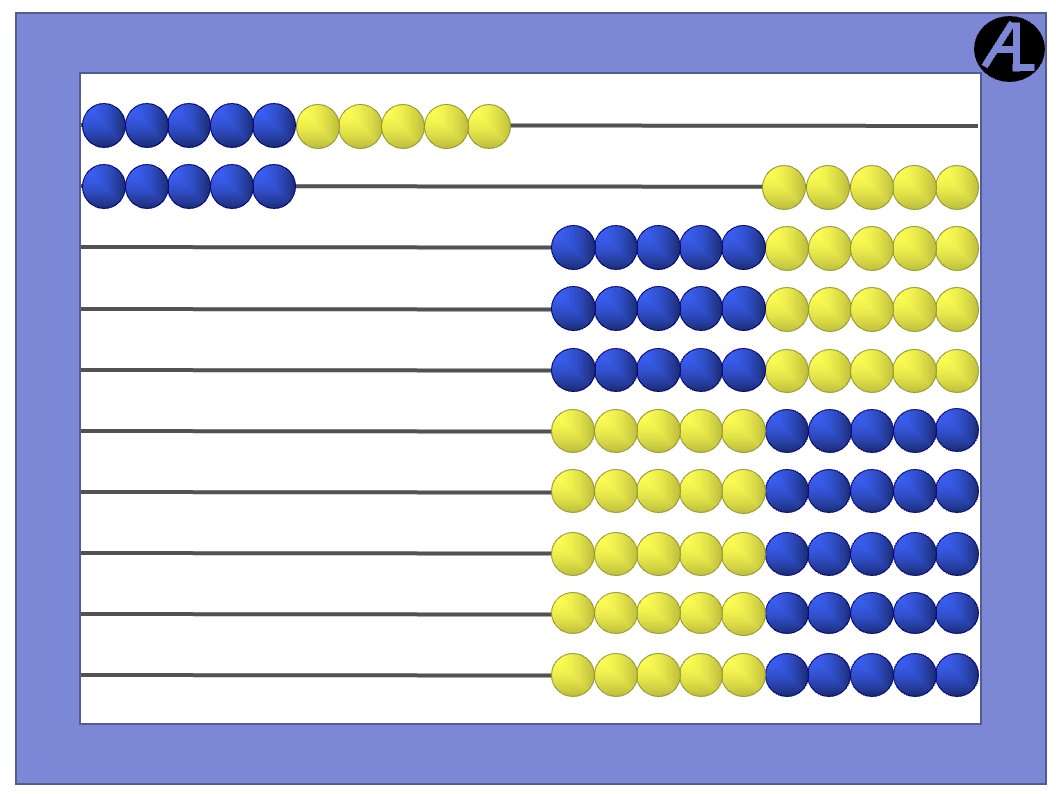
Facts practice should always provide a strategy for the learner to figure out a forgotten answer. The Cotter Abacus provides a good way through visual representation, based on 5s and 10s.
A 5-year-old was asked how much is 11 and 6. After he said 17 without counting, he was asked how he knew. He replied with a grin, “I have the abacus in my mind.”

What about multiplication math facts? My understanding is that they have to be memorized.
Hi, Melissa.
There is a huge difference between learning multiplication math facts and rote memorizing them. If my child is able to get to the answer by using strategies such as picturing the abacus in their mind or using strategies to get to the answer, doesn’t that produce the same result: getting the correct answer to the multiplication math fact.
However, what if a student is unable to memorize? Does that mean they cannot do multiplication? No. I have one child who is unable to memorize – and he learned his multiplication math facts! How!? Because he applied the strategies taught in RightStart Math to find the answer. He knew how to think about multiplication in such a way that he was able to get to the answers. Isn’t that what we want of our children? We want them to think.
When I was in school, I only used rote memorization to learn the multiplication math facts. Now, as an adult, I sometimes forget which answer goes with which math fact. However, because of RightStart Math, I can figure out the answer – even when my memory fails!
Thank you, RightStart Math!
More than 20 years ago, I listened to Dr Cotter speak at a homeschool conference and suddenly I understood math concepts I had never understood despite being an “A” math student my whole life. I used RightStart with all of my older children who all understood by using the Cotter abacus. I was lured away by another program with my youngest son who struggled until I went back and pulled out the Cotter abacus (it is different than others), fraction mat, and RightStart math games I had used with his older siblings. I am a twenty-five year veteran homeschool mom and have seen the proof of RightStart.
I find that even though my children understand the concept of multiplication they take a long time to recall the products. I am tempted to use multiplication flashcards.
Hi, Danyella.
It is very tempting to resort to flashcards! After all, that is how I learned when I was younger. However, if you were to ask most people who have math anxiety, they will say that they have math anxiety because of the flashcards and timed tests.
Instead of flashcards, have your children play games. The same result is accomplished – but without the extra stress that flashcards can create.
By the way, I loved flashcards and worksheets. Why is that? Because I knew the answers! It made me feel good. However, I saw many of my peers freeze when shown a flashcard, and the reason was that they were not confident with the answers. There is nothing in showing that flashcard that will help the student get to the answer, except for the mom eventually giving them the answer.
When playing math card games, the student should have their manipulative handy – to look up any math fact they do not know.
Have a fabulous day – and play a math card game!