Dr. Cotter on Fractions

Fractions have a bad reputation as being incomprehensible and unpredictable. Cartoons and jokes exploit this fear of fractions for amusement. Believe or not, it’s all a huge misunderstanding.

Fractions are amazing.

Fractions are necessary.

Fractions are needed, among other things, for telling time, for counting money, and for cooking. 

The word fraction comes from Latin “frangere” meaning “to break.” So, historically, fractions were considered only as a part of a whole. This meant they could never be equal to or greater than one. For example, one third meant one of three equal parts of an object.

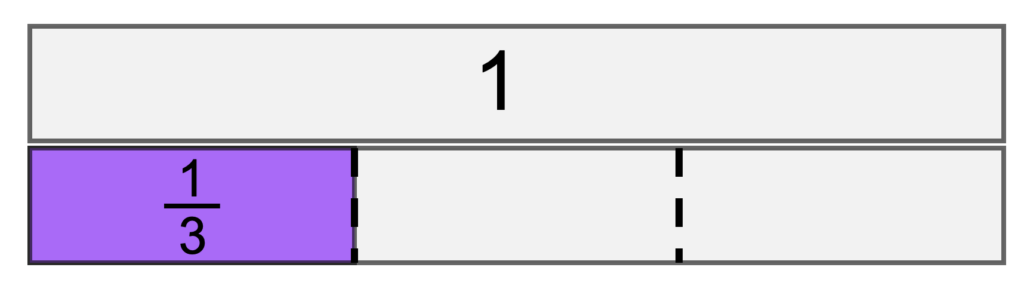
Then in the 1600s, mathematicians expanded the fraction concept. Its “new” interpretation is the division of any two whole numbers. Thus, one third can be thought of as 1 divided by 3.

This means 3/3 is a now a fraction because it is 3 divided by 3, even though it is equal to one. And 2/3 can be thought of as 2 divided by 3. 

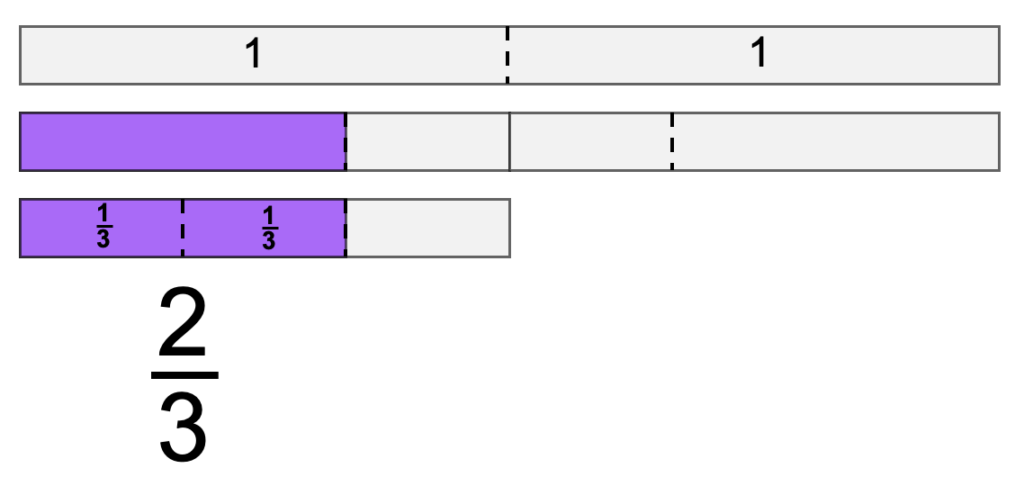
Some people didn’t exactly welcome these new fractions. They called their old familiar fractions proper and the new unfamiliar fractions improper. The term improper seems to imply that something is not quite right, but it merely means improper fractions were not part of the traditional or original set of fractions.

Most of the time, nobody cares if a fraction is proper or not.

In everyday language, unfortunately, we still use the centuries-old idea of a fraction. A small amount of something is referred to as a fraction of it. Even the dictionary says a fraction is a tiny part. The Thesaurus lists words such as “fragment” or “snippet” as a synonym for fraction. Thinking of fractions in this limited fashion is detrimental for a complete understanding.

One goal in teaching math is to help the child see relationships between concepts. To help children in their mathematical understanding, we need to teach fractions as division much sooner. Interestingly, one early link of fractions to division emerged from remainders in division.

Circular Fraction Model

One of the earliest models used for teaching fractions was the circle. However, circles do have some serious drawbacks. While it’s easy to see 1/2, 1/3, or 1/4 of a circle, it’s not easy to see 1/7, 1/8 or 1/9 or to visualize the differences.

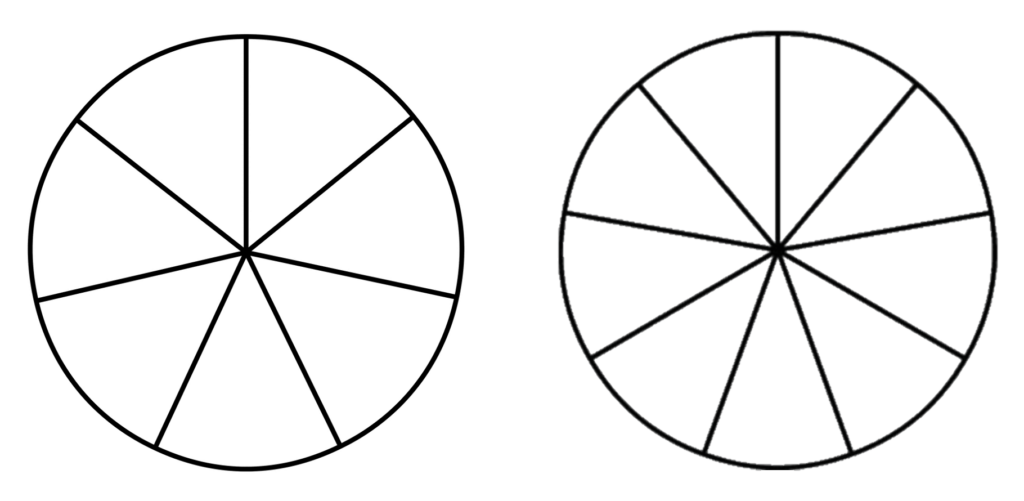Trying to draw or compare fractions with pies is difficult because we tend to view quantities in a straight line, not around a ring. Also, attempting to compare slices in two circles merely gives our eyes lots of exercise. Another serious drawback of the circle model is the difficulty in showing fractions greater than 1. 

Linear Fraction Model

A better visualizable fraction model is fraction strips.

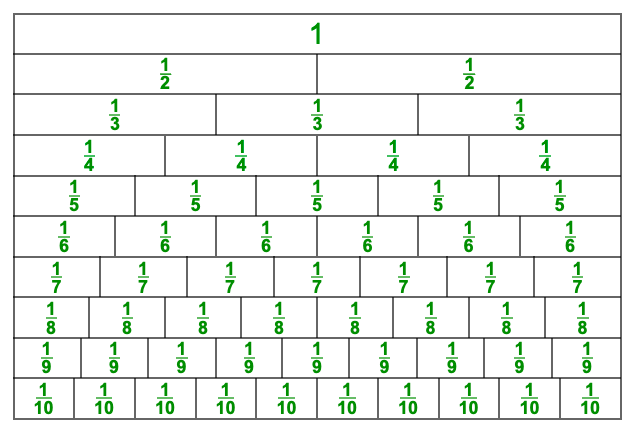
They are a series of ten rectangles, each about 8 to 10 inches long.

• The first rectangle has 1 written in the center.
• The second rectangle has a vertical line dividing it in half with 1/2 written in the centers of the two sections.
• The third rectangle has two vertical lines dividing the strip into thirds with 1/3 written in all three sections.

This pattern continues for the remaining rectangles to the tenths. The ten rectangles placed in order adjacent to and under each other form the fraction chart.

You may have seen variations of this chart with each fraction in a different color. At first, this might seem to be a nice enhancement. However, when the strips are assembled into the fraction chart, the colors become more of a focal point than the size of the fractions.

Fractions must be identified by their differences in size, not by their color.

Therefore, all the rectangles must be the same color.

Another strange variation is the absent fractions. The sevenths and ninths go missing, but the twelfths are tossed in. Since when do we dismiss numbers we don’t like?

When the fraction chart is complete, there are some interesting arcs, actually hyperbolas. When some strips are missing, the hyperbolas disappear.

It is best to have two sets of fraction strips, one kept intact as the fraction chart and the other set cut into individual pieces. Children benefit by assembling the strips into the chart like a jigsaw puzzle. Young children love to do it over and over. Have them build the fraction chart next to, not on top of, the model.

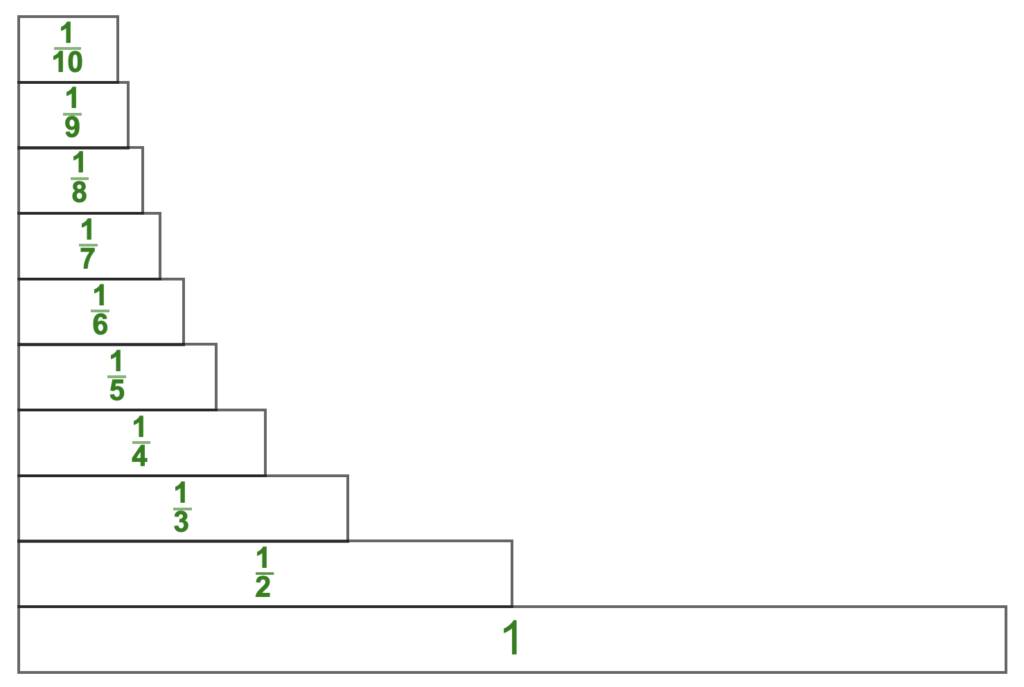
Another intriguing activity is to take one strip of each size and build the stairs.

The Mike Story

Some years ago, I tutored Mike, a third grader, who needed help in math. His family was moving out of the area, so on the last day I introduced him to fractions. I started by asking him to assemble the puzzle. After explaining what 1/4 meant, I asked, “Which is more, 4 or 5? But which is more 1/4 or 1/5? Which is more 2 or 3? 1/2 or 1/3?”

Then I continued with: “How many thirds do you need to make a whole? How many fourths? How many fifths?” Next I explained that 3/4 was three 1/4s.

At the end of the 45-minute session, I told Mike that he hadn’t learned everything about fractions. I said that we did not talk about adding fractions like 1/4 plus 1/8. Mike looked at the chart and announced the answer as 3/8. He had done it in his head!